Brier Scores
POLS 3220: How to Predict the Future
Today’s Agenda
What is the best way to evaluate probabilistic predictions?
Introduce Brier Scores, the method we’ll use to assess accuracy in our forecasting challenge this semester.
Warmup
Was this a bad prediction?
“There’s no chance that the iPhone is going to get any significant market share. No chance.”
—Steve Ballmer, Microsoft CEO, 2007

Warmup
What about this prediction?
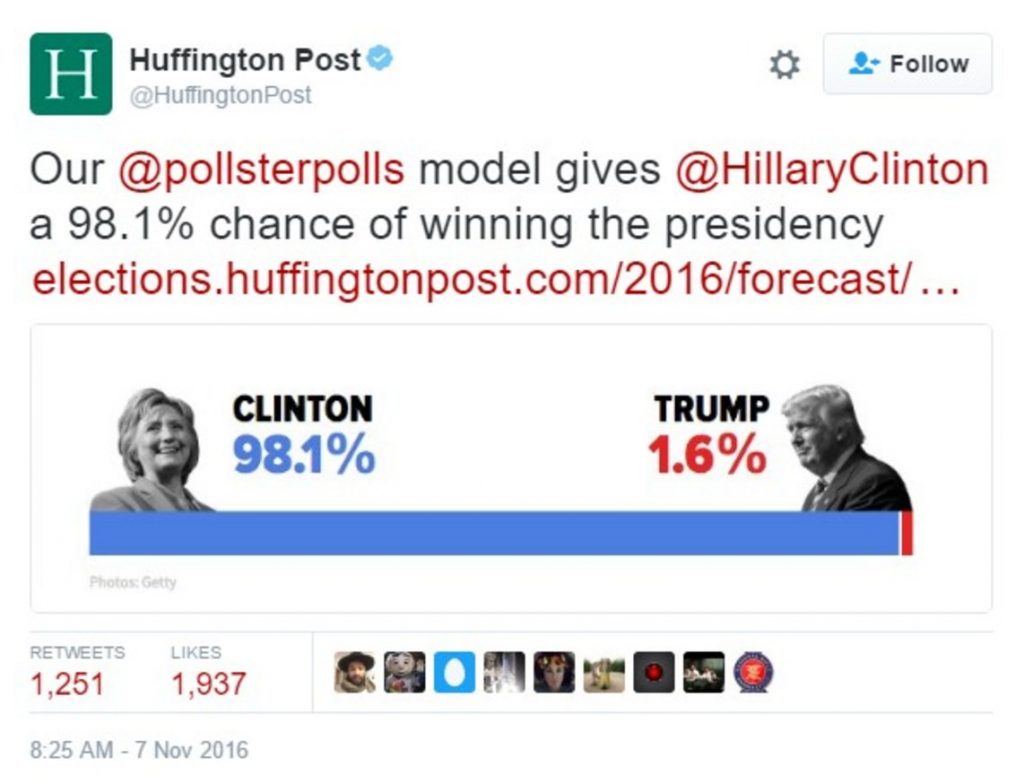
Warmup
What about this one?
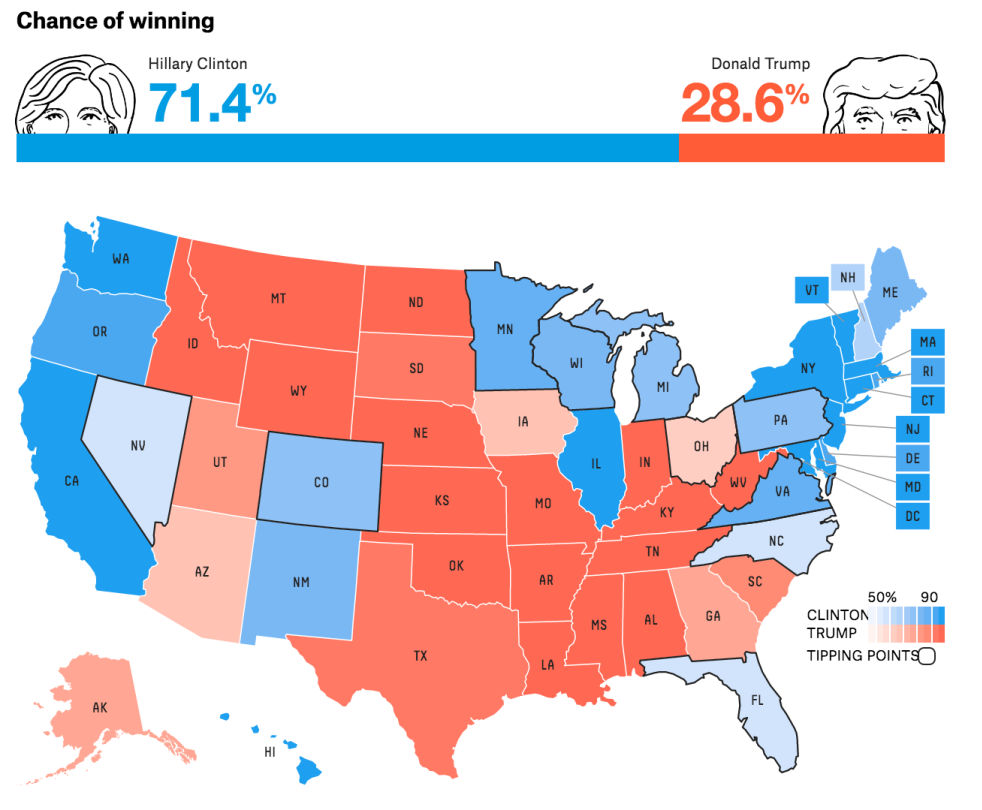
Scoring Predictions
Evaluating individual probability statements is quite tricky.
If something happens that the forecaster said was unlikely, was the forecaster wrong or unlucky?
Much better to evaluate a forecaster’s track record over many predictions.
- When the forecaster says 70% chance, does the event happen about 70% of the time?
Calibration
Across thousands of predictions about politics and sports, Nate Silver has a pretty impressive track record…
Scoring Predictions
Calibration isn’t the only thing we care about, though.
A doctor who tells his pregnant patient there is a 50% chance the baby will be a boy is perfectly-calibrated…but the forecast isn’t terribly useful.
The ultrasound tech who can predict with100% confidence is much more useful. Same level of calibration though!
We want forecasts that are both well-calibrated and as confident as possible.
Scoring Predictions
- Consider a scoring system where we evaluate predictions based on average error.
- This has some nice properties: you score better if you are confidently correct, and score worse if you are confidently incorrect.
| Prediction | Outcome | Error |
|---|---|---|
| 70% | 1 | 0.3 |
| 20% | 0 | 0.2 |
| 70% | 0 | 0.7 |
| 40% | 1 | 0.6 |
- But there’s a huge problem with this scoring system…it encourages lying!
Average Error is a Bad Score
Suppose you are a TV meteorologist.
Your weather model says it’s going to be a rainy week. 80% chance of rain each day.
What do you report to your viewers if you want the best average error for the week?


Average Error is a Bad Score


Average Error is a Bad Score


Average Error is a Bad Score


Average Error is a Bad Score


Brier Scores
We would like a scoring rule that encourages honesty (a strictly proper scoring rule).
Penalizing extremely wrong predictions helps.
The Brier Score does this by taking the average squared error (Brier, 1950).
Why Squared Error?
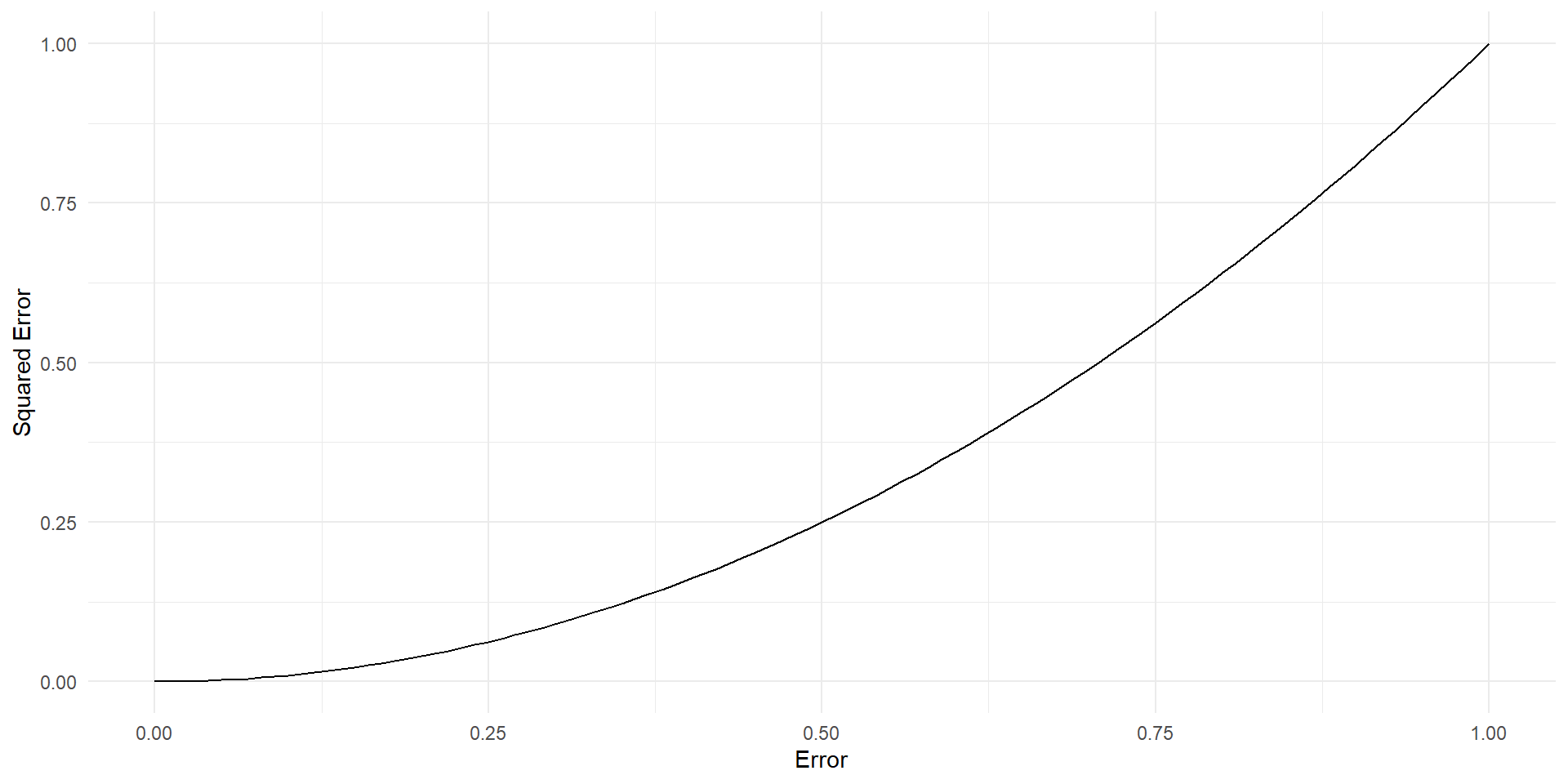
Notice that the penalty is particularly steep when predictions is wrong and overconfident.
Brier Scores


Brier Scores


Brier Scores


Brier Scores


Brier Scores


Brier Scores


Key Takeaways
Brier Scores are a sort of mathematical truth serum.
Your optimal strategy in the forecasting challenge is to report your honest beliefs.
A forecaster’s expected Brier Score cannot be improved by exaggerating or hedging probabilities.
