How To Predict The Future – Conditional Probability

Today’s Agenda

Learn how to estimate conditional probability
Introduce a common approach used by successful forecasters: balancing Inside View and Outside View.
Show how all this connects to a central problem in statistics: the bias-variance tradeoff.

Warmup

Motivating Problem

Will the movie Digger be “Certified Fresh” by Rotten Tomatoes?

Discuss: How would you go about this prediction? What would be the first piece of information that you research?

Two Different Approaches

Inside View: Focus on the details of the case at hand.
- What characteristics of Digger suggest that it will be Certified Fresh?
Outside View: Ignore the details of the case at hand. Focus on what happened previously with similar cases.
- How often does any film achieve a Certified Fresh rating?
Most people naturally gravitate towards the Inside View (Kahneman and Lovallo 1993), but the best forecasters combine both approaches!

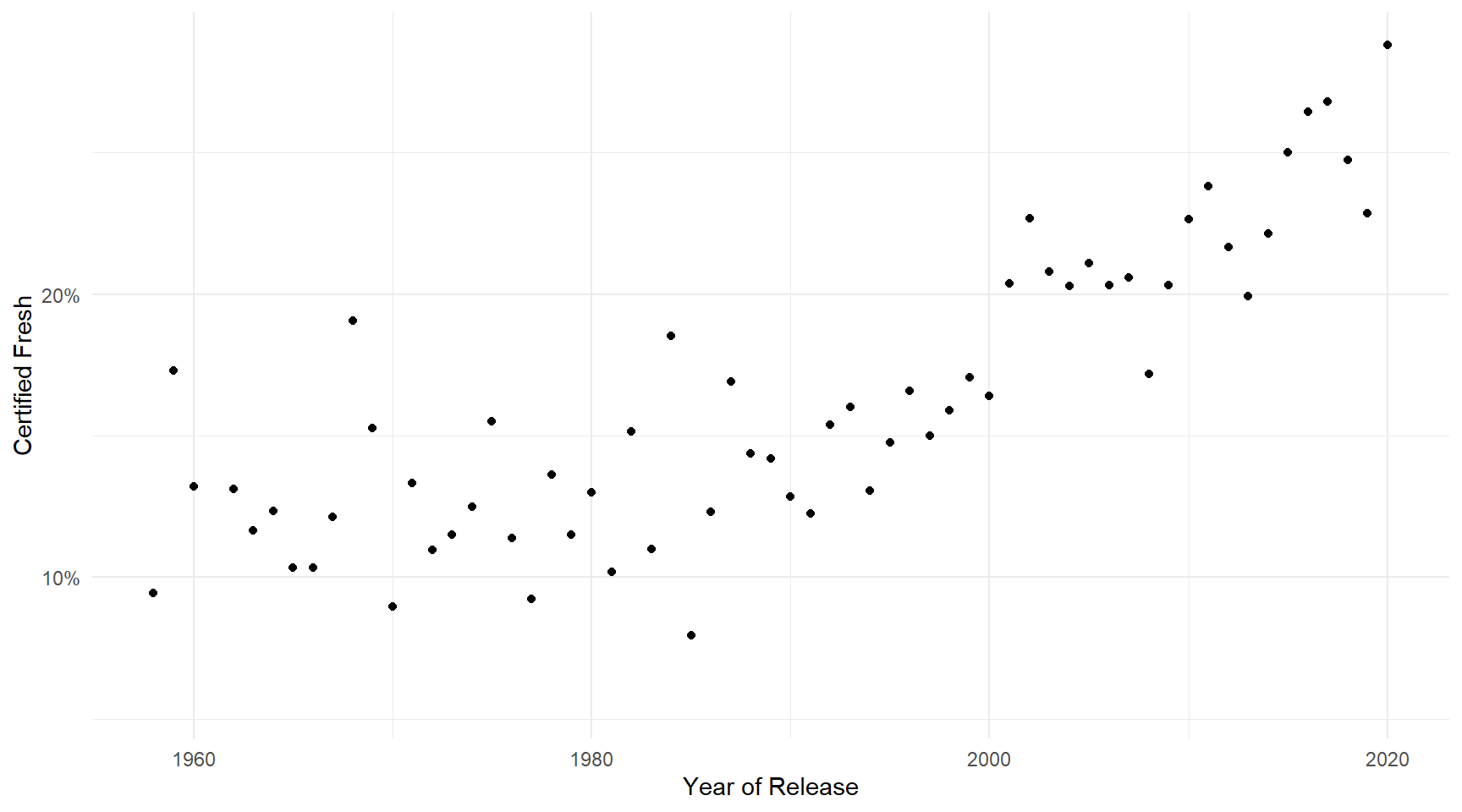
Outside View

Tomatometer	Total	%
Certified-Fresh	3,259	18.4
Fresh	6,844	38.7
Rotten	7,565	42.8

Outside View

This base rate is a useful starting point.
- Achieving a Certified Fresh rating is historically very rare. Serves as an “anchor” for our prediction.
What’s the problem with this approach? Why not stop there?
- The pure Outside View yields a biased prediction, because it doesn’t incorporate any information about the case in question.
- More details about the movie Digger should help us refine our prediction.

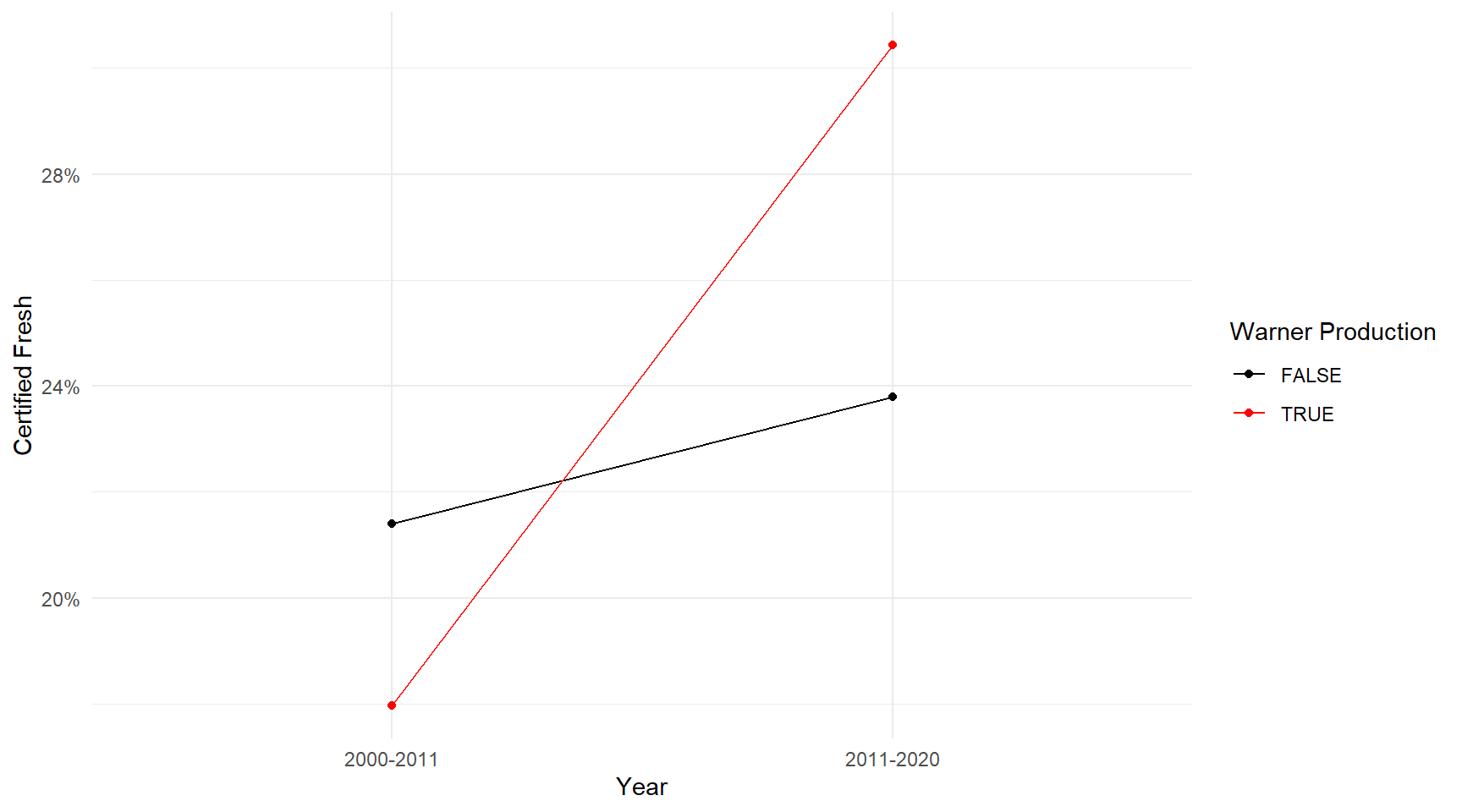
Unconditional Probability

Conditional Probability

How far should we take this???

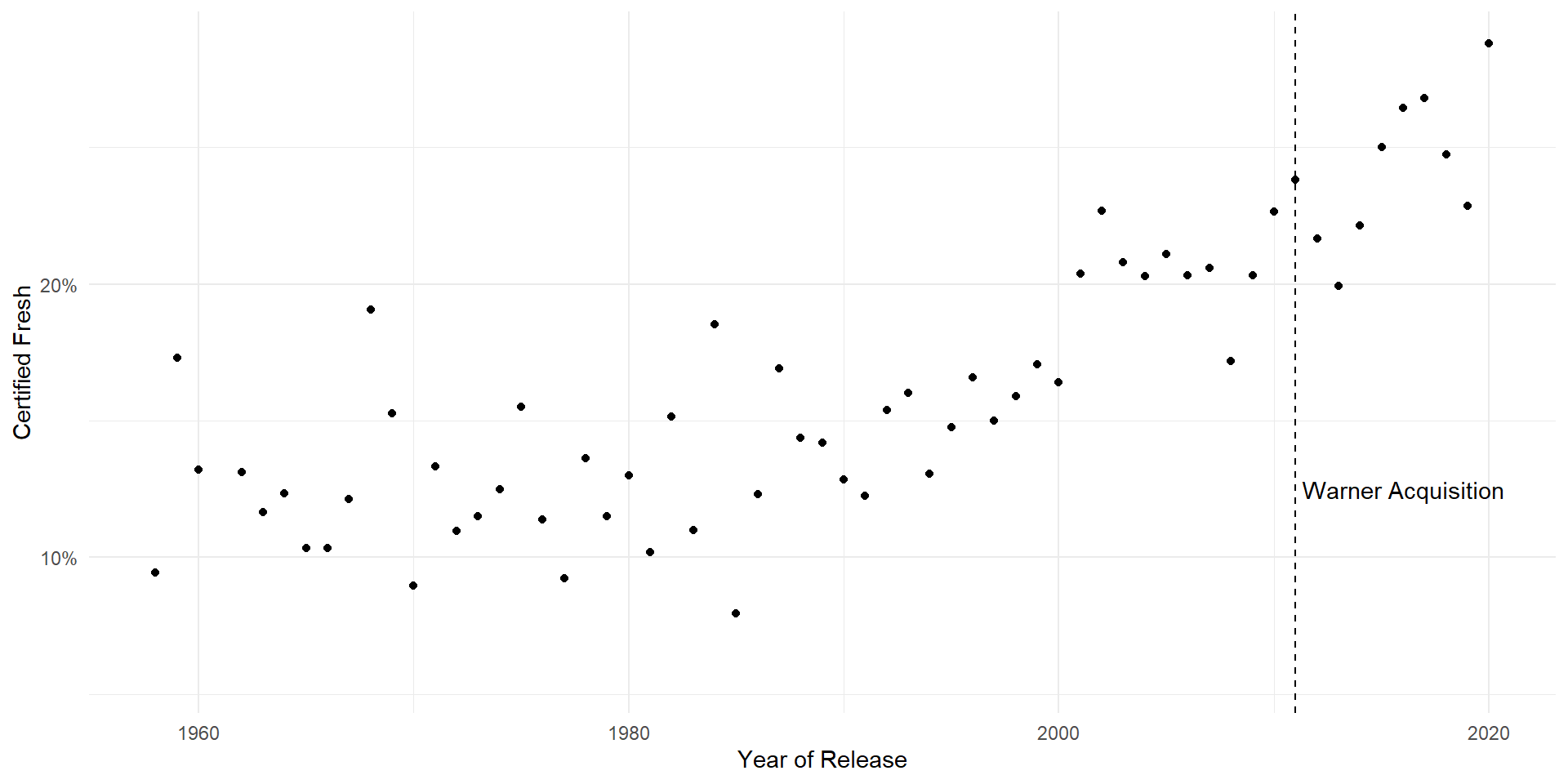
Inside View

The “Inside View” is very confident about Digger. English-language films directed by Alejandro Iñárritu are always Certified Fresh.
What’s the problem with this approach?

Inside View

Well, there are only 3 English-language films in the entire database directed by Alejandro Iñárritu.

Practice

What is the chance that he just got lucky?

If Iñárritu’s true probability of success was 60% (slightly better than a coin flip), what is the probability that all three of his English-language films would be Certified Fresh?

Practice

Inside View

With only three data points, we cannot claim with confidence that Iñárritu’s next English-language movie is guaranteed to be Certified Fresh.
It could be that his movies are guaranteed hits.
But he also could have gotten lucky.
In all likelihood, the evidence reflects some combination of skill and luck.

Bias-Variance Tradeoff

On one end of the spectrum (pure Outside View), we have a biased but precise prediction.
- 18.5% of all movies are Certified Fresh.
On the opposite end (pure Inside View), we have an less-biased but highly uncertain prediction.
- 100% of Iñárritu’s English-language films have been Certified Fresh (3 for 3).
The truth probably lies somewhere in the middle.
The “art” of forecasting is learning how to balance this tradeoff. How much should you weigh the Outside View vs. the Inside View?

Bias-Variance Tradeoff

Next Time

Bayes Rule as a method for computing conditional probability, and adjusting your predictions in light of available evidence.

References

Kahneman, Daniel, and Dan Lovallo. 1993. “Timid Choices and Bold Forecasts: A Cognitive Perspective on Risk Taking.” Management Science 39 (1): 17–31. https://www.jstor.org/stable/2661517.