Jury Theorems

POLS 3220: How to Predict the Future

Warmup

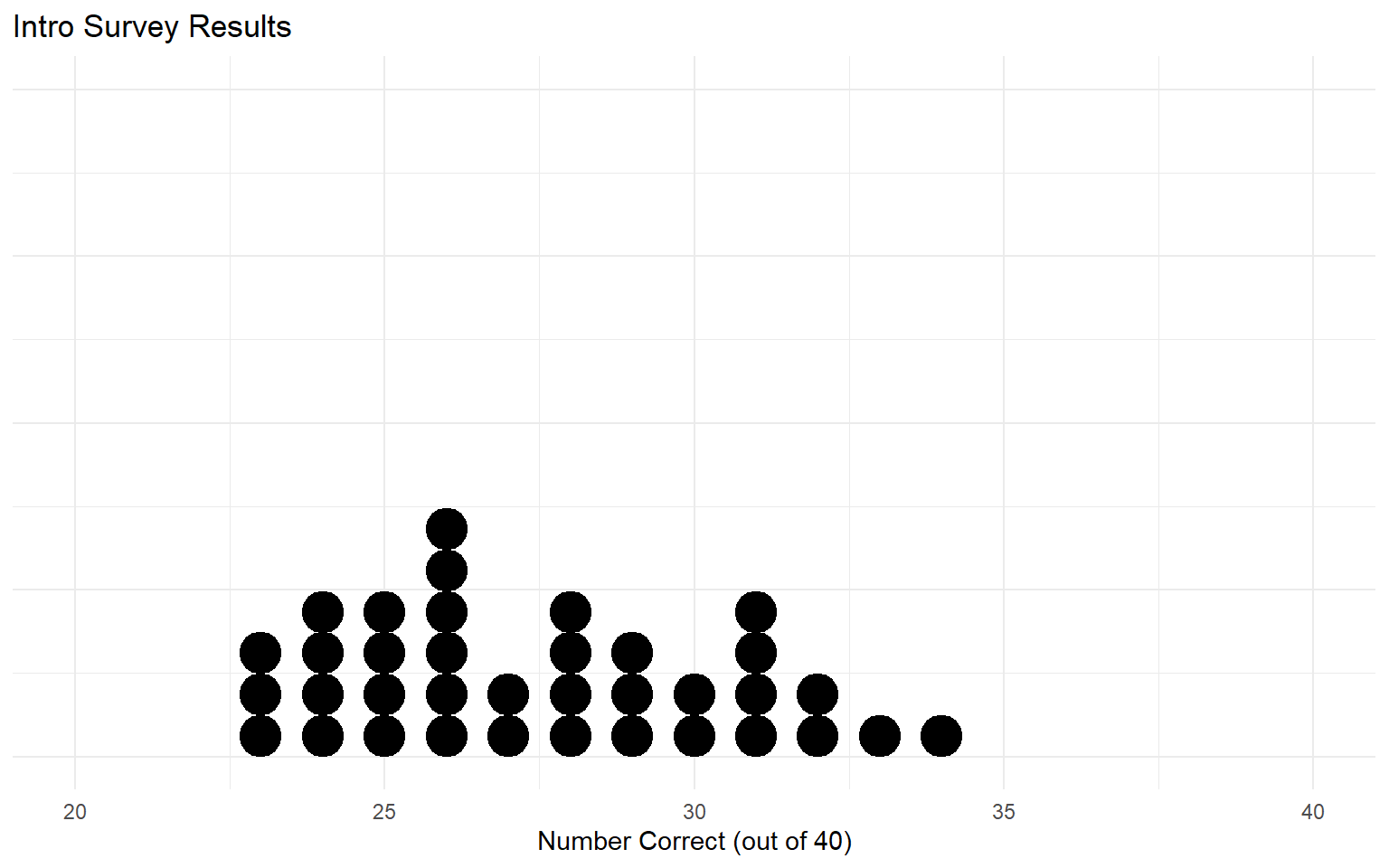
Warmup

Warmup

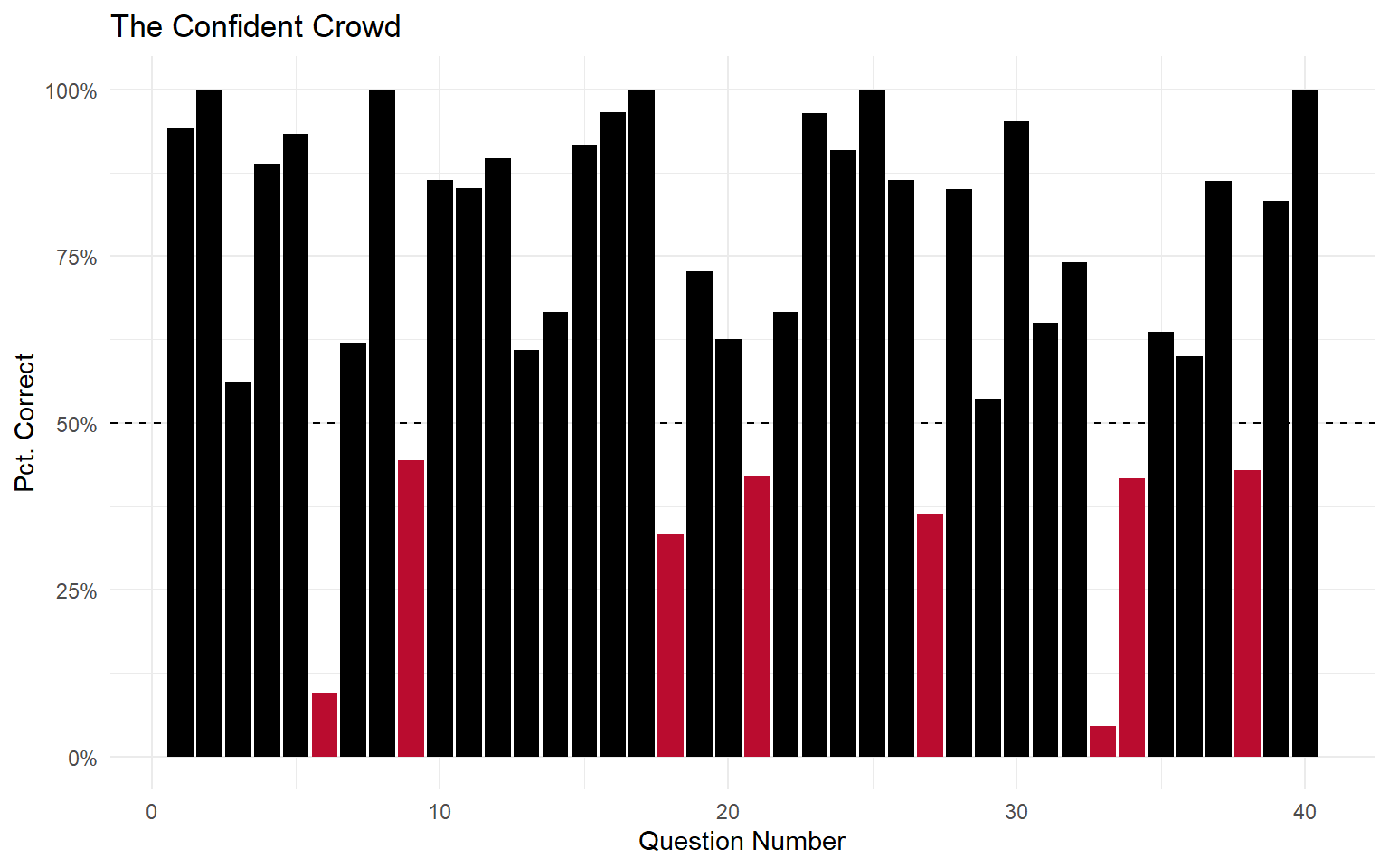
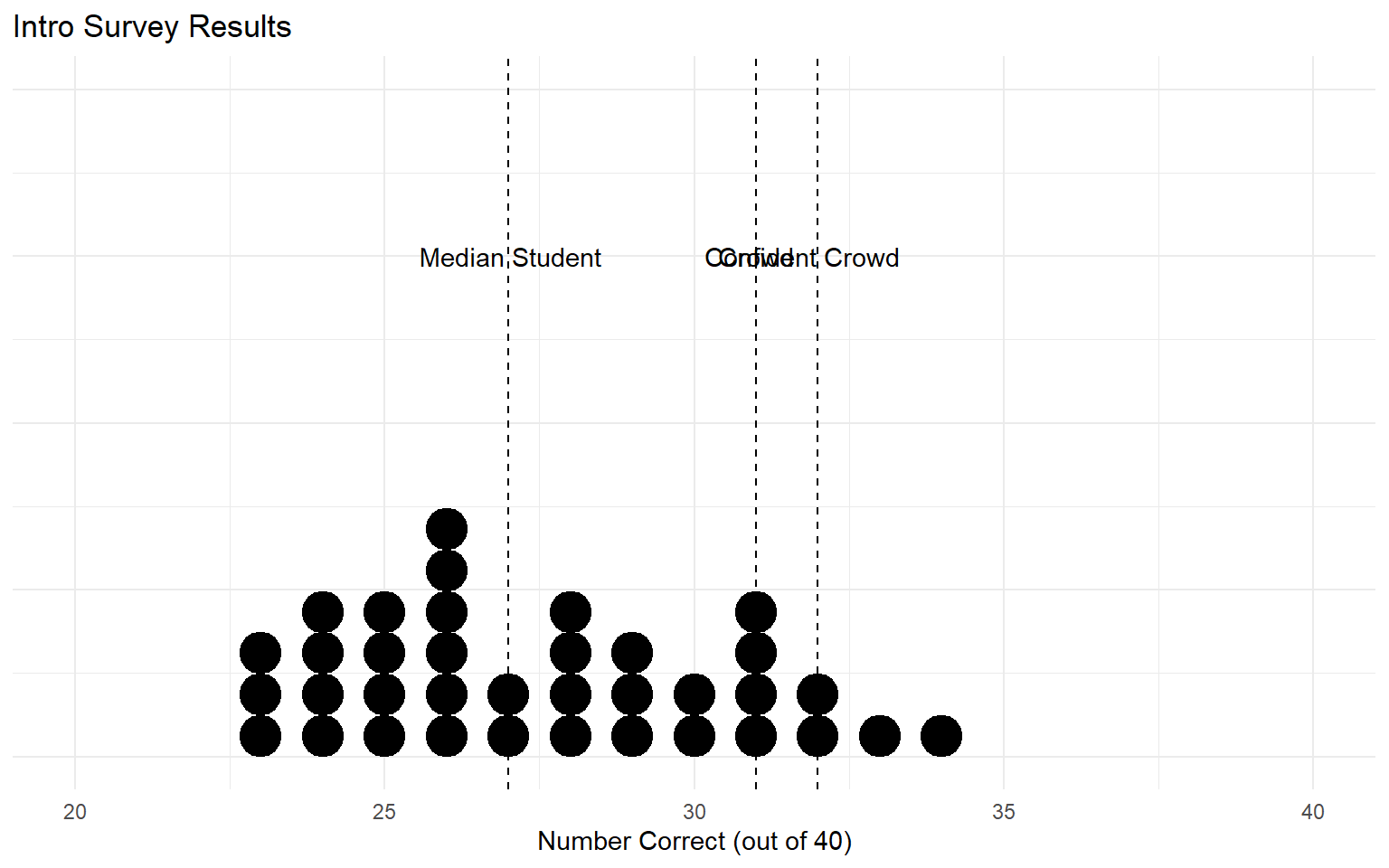
Ponder: What if I asked the class to vote on the answers? How many correct answers do you think the majority would get?

Warmup

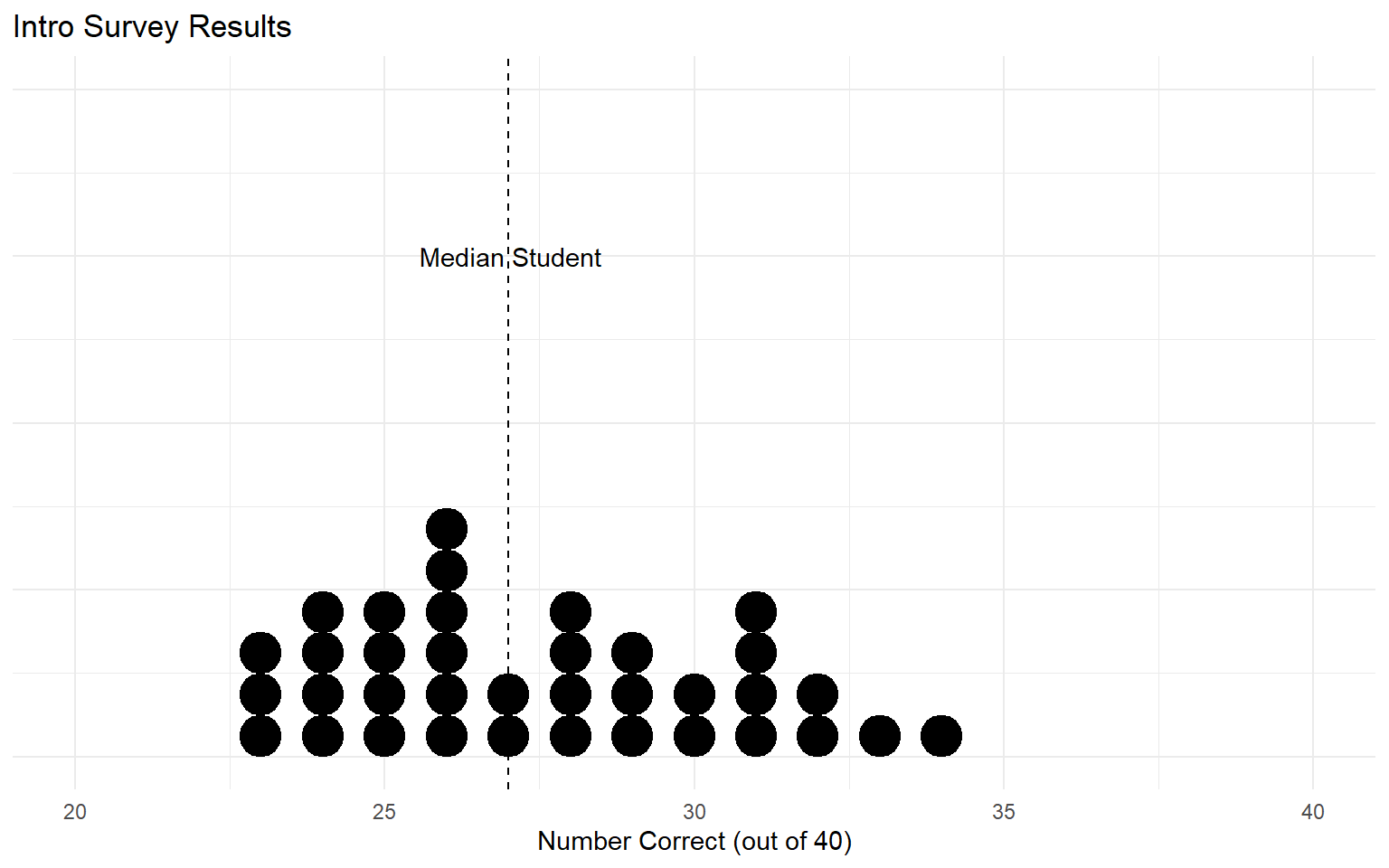
Warmup

Warmup

Ponder: What if I only took the majority vote of students who were really confident in their answers (>95%)? Would that result be better or worse?

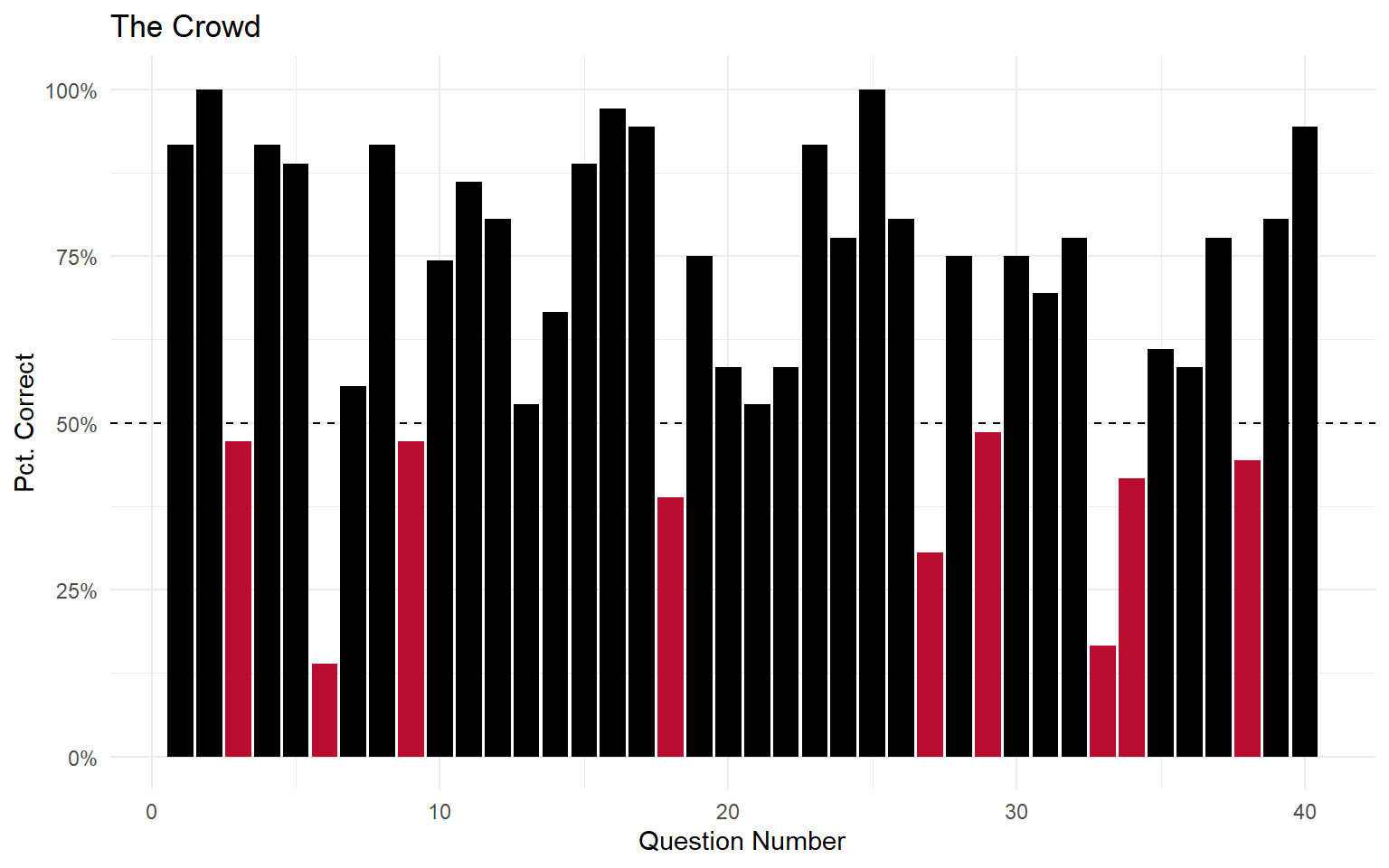
Warmup

Warmup

Wisdom of Crowds

• This phenomenon is known as the Wisdom of Crowds.

  • Groups of people often outperform the individuals that make them up.

• Over the next few weeks, we’ll discuss how to harness the Wisdom of Crowds to make better predictions.

• We’ll also explore the conditions under which groups of people perform worse than individuals (the Madness of Crowds).

Marquis de Condorcet (1743-1794)

Condorcet Jury Theorem

Assumptions:

• A group is voting on a binary (Yes/No) decision.

• Each voter has probability \(p > \frac{1}{2}\) of making the correct choice.

• Individual votes are independent of one another.

Theorem:

• As the size of the group \(n\) gets large:

  • The probability that the majority makes the correct choice approaches 100%.

Condorcet Jury Theorem

Ponder: Does the Condorcet Jury Theorem remind you of anything?

Condorcet Jury Theorem

Example: A jury with 5 members, where each individual has a 60% probability of choosing the right answer.

Condorcet Jury Theorem

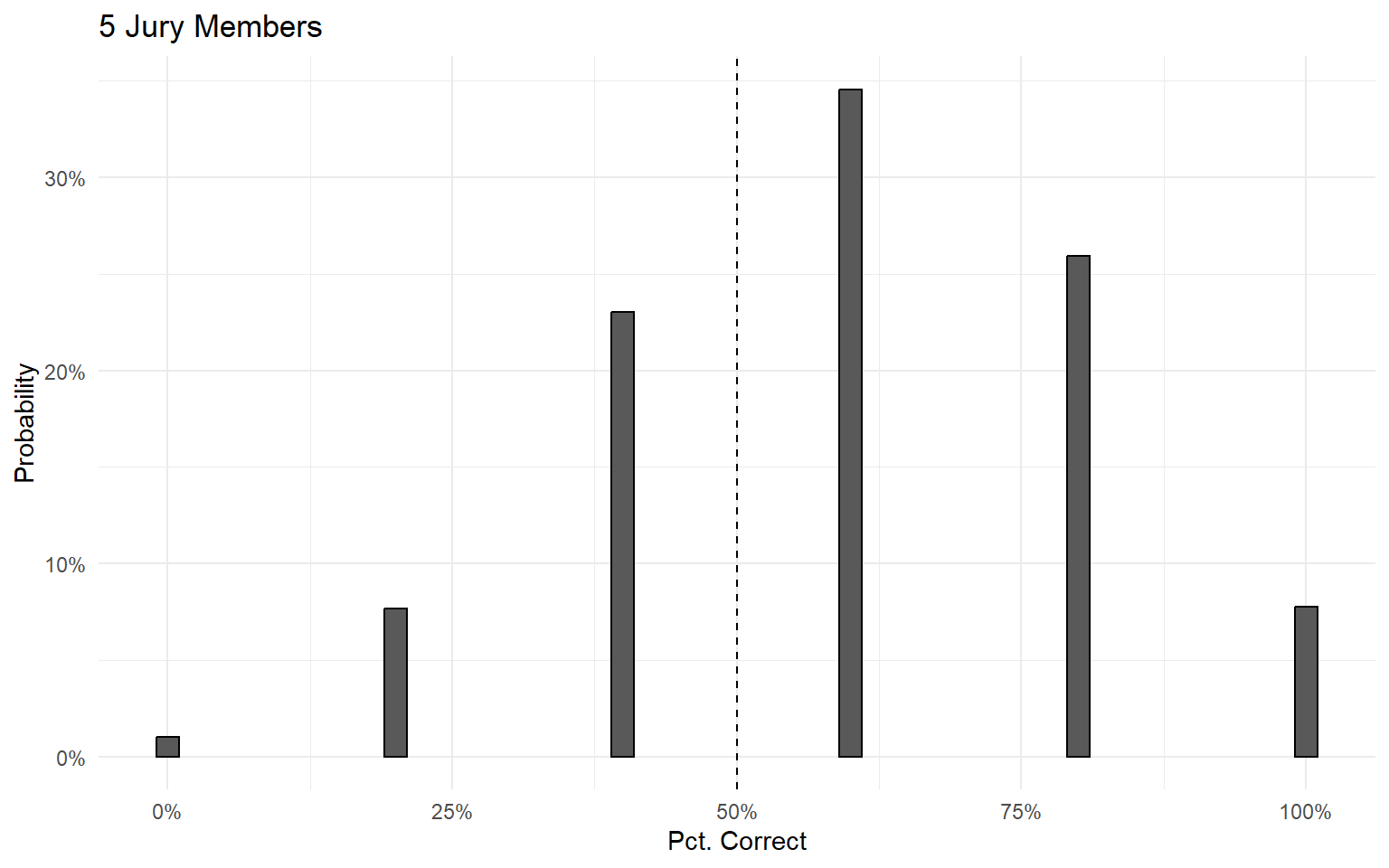
Condorcet Jury Theorem

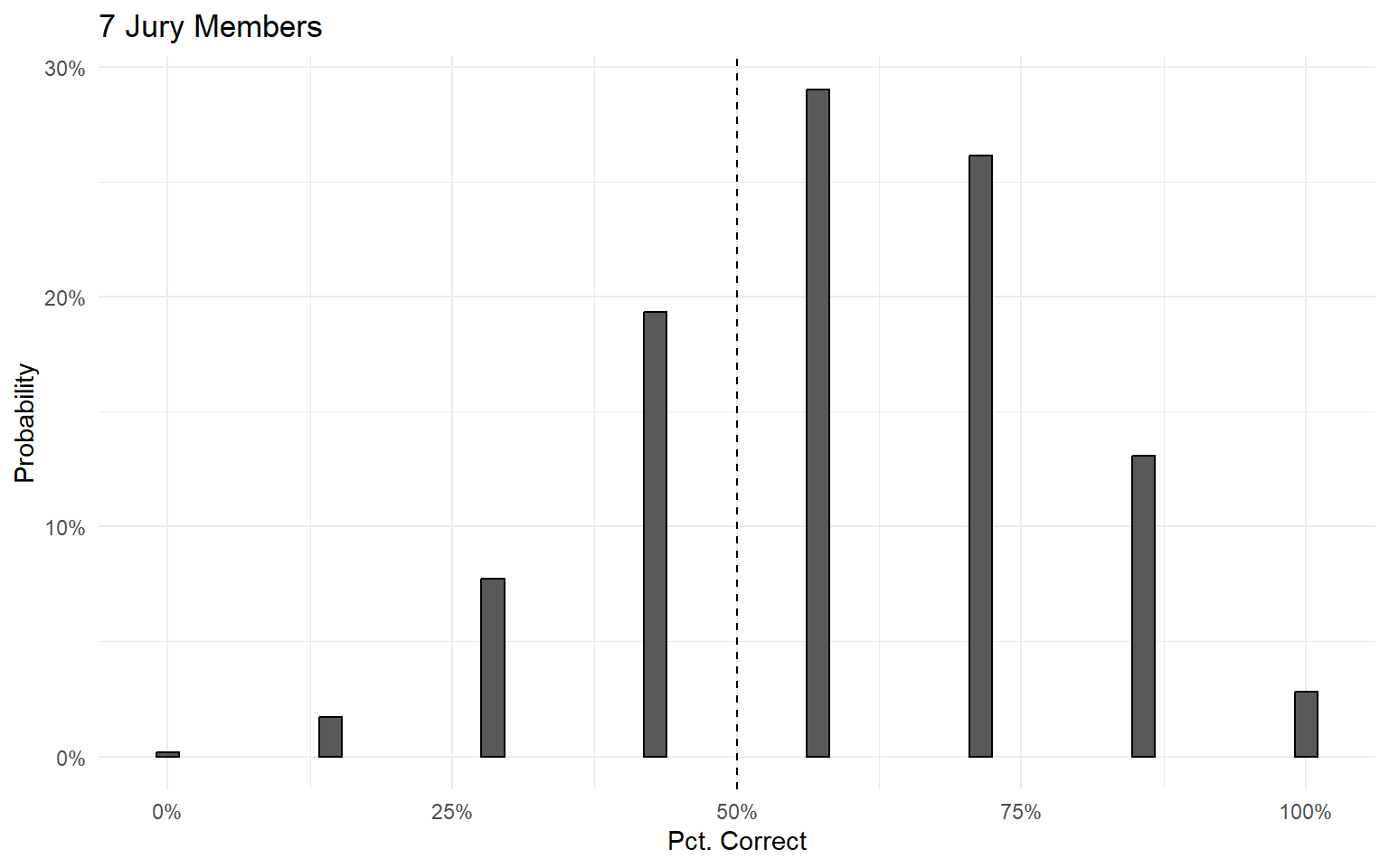
Condorcet Jury Theorem

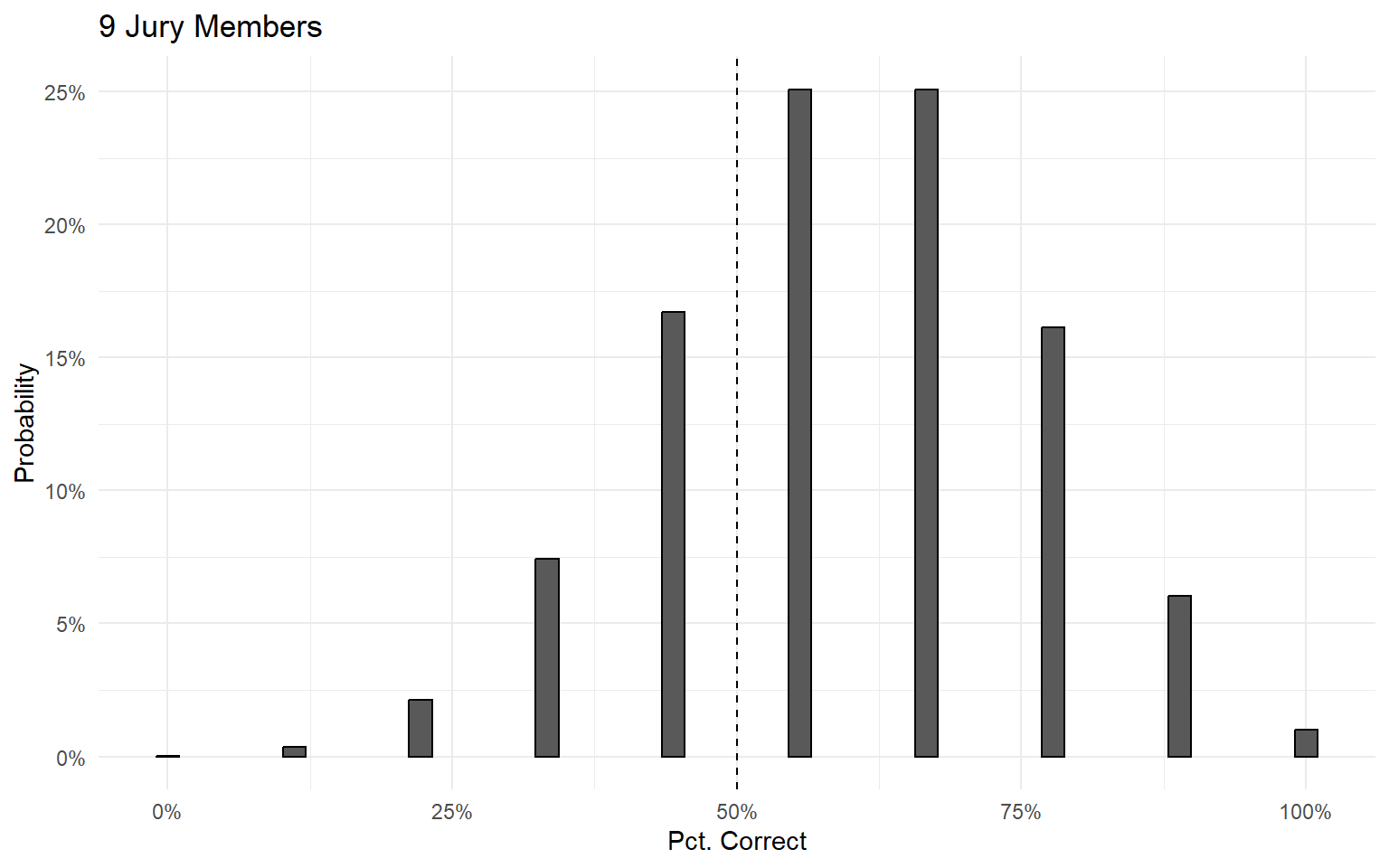
Condorcet Jury Theorem

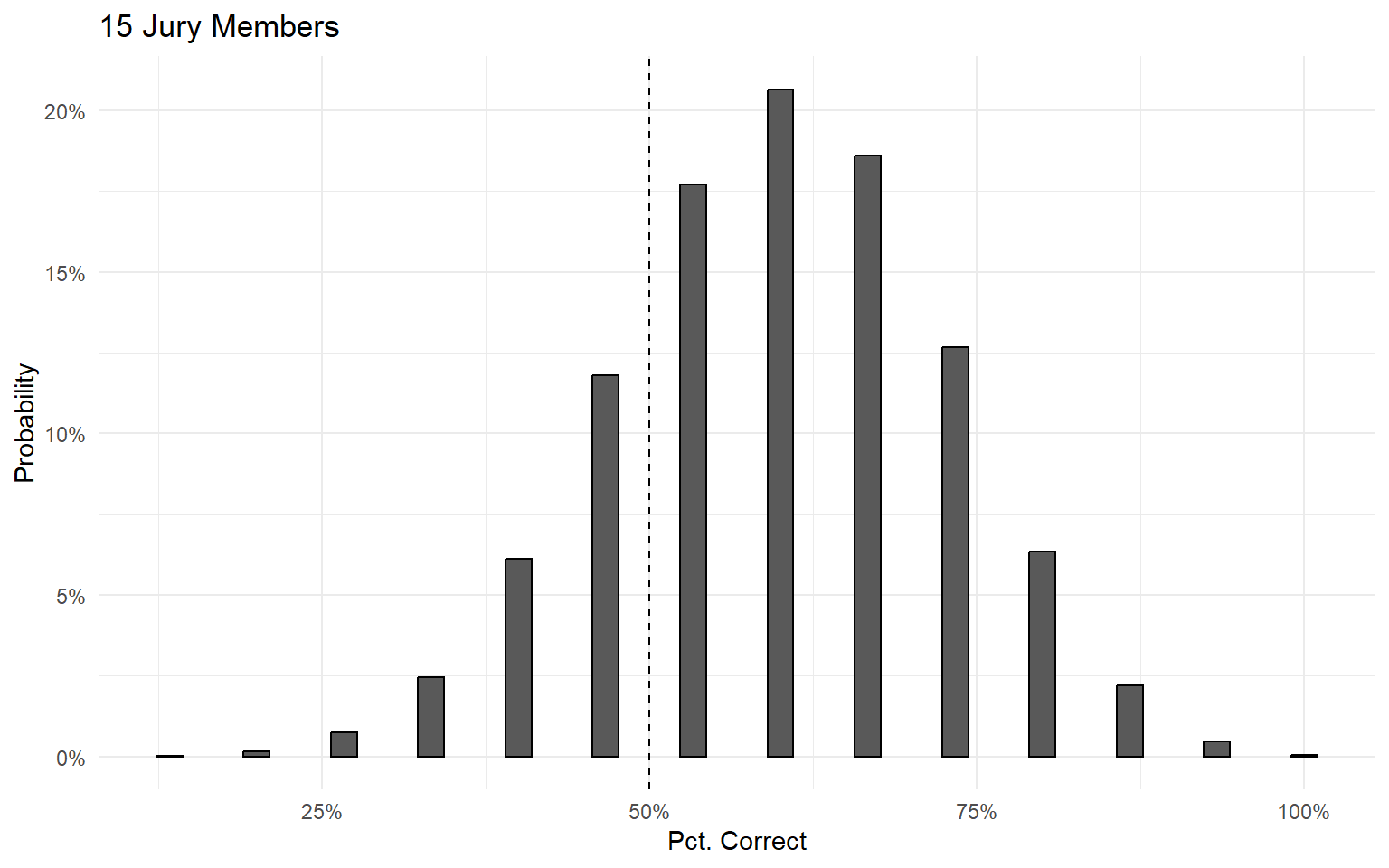
Condorcet Jury Theorem

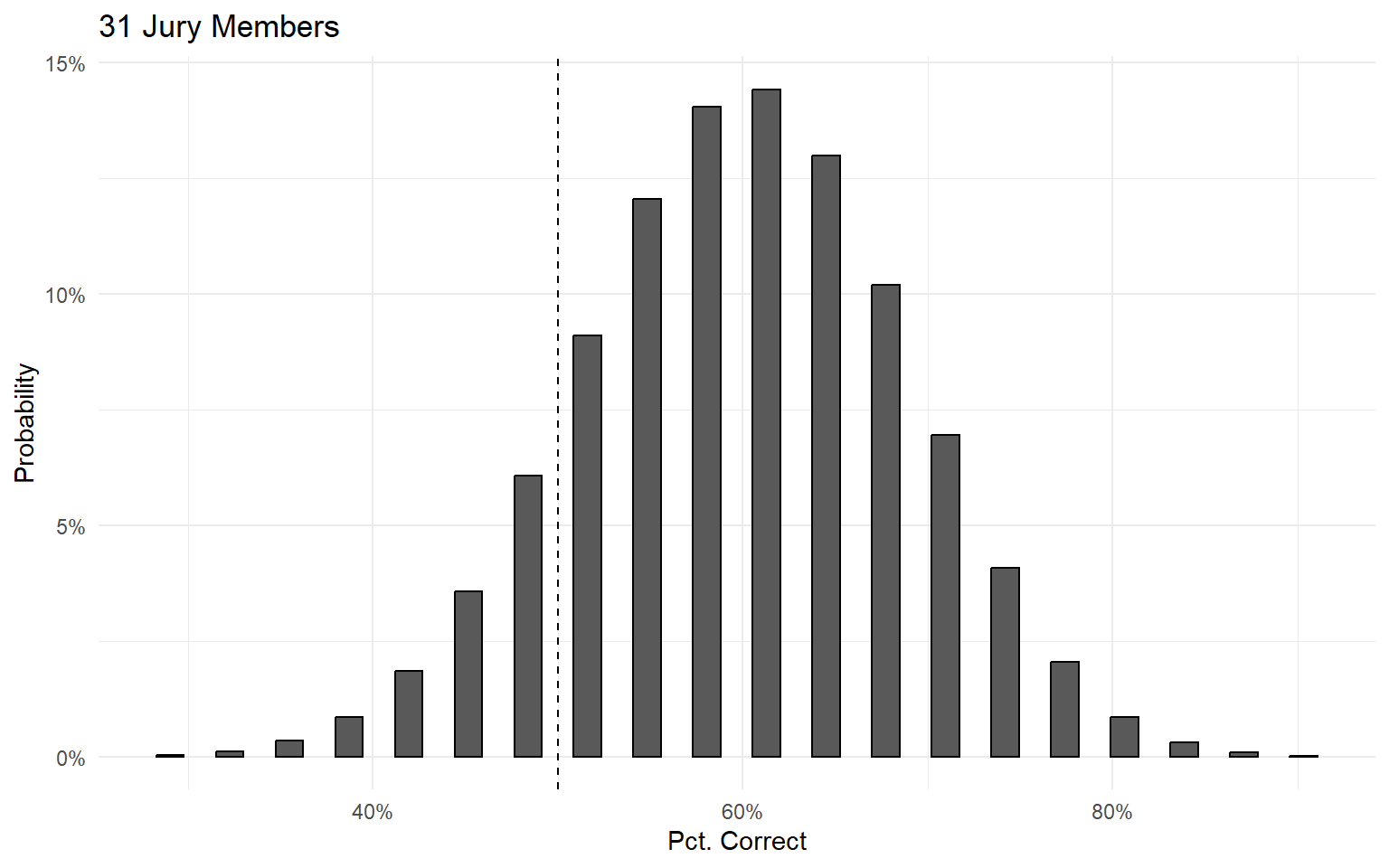
Condorcet Jury Theorem

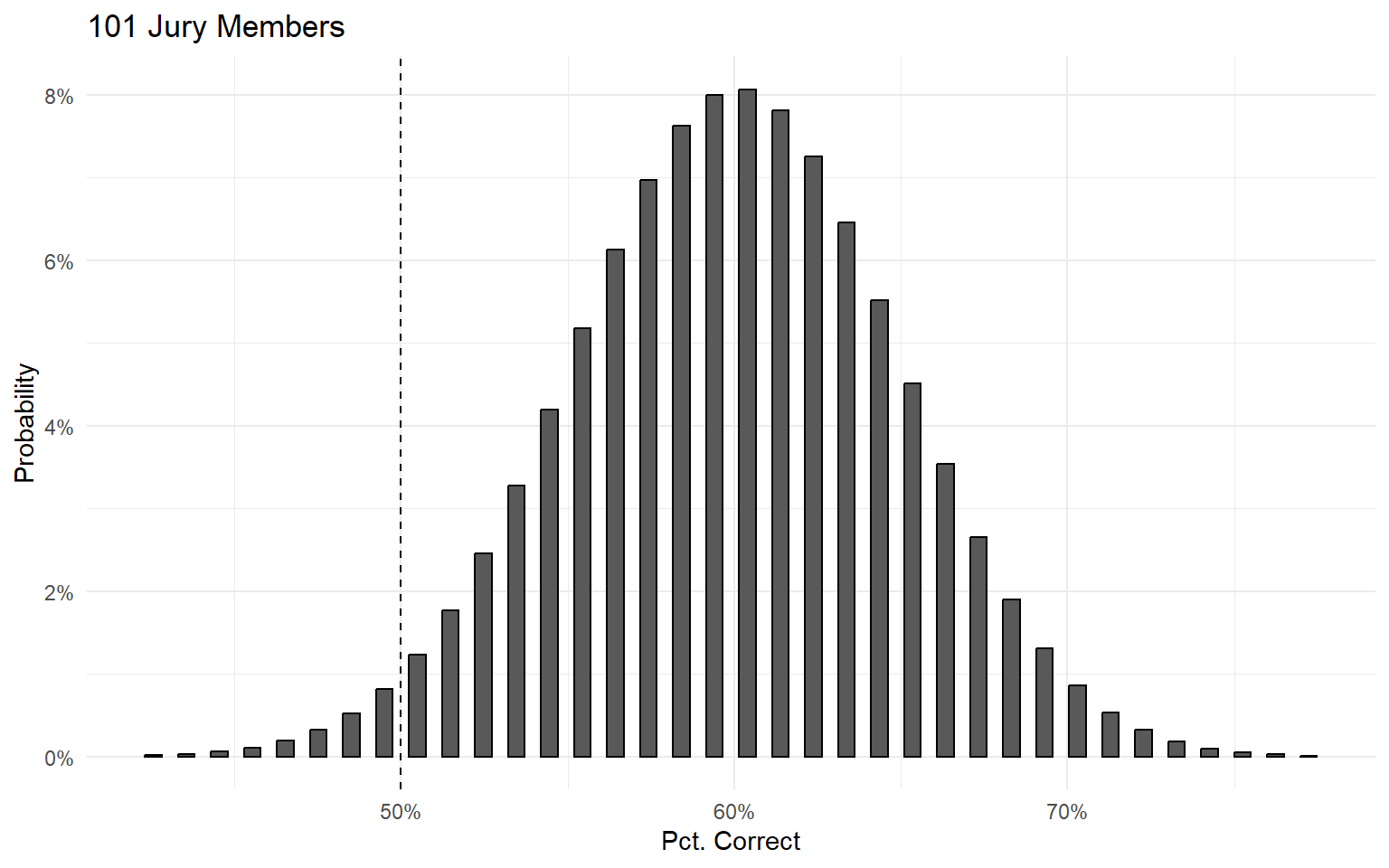
Condorcet Jury Theorem

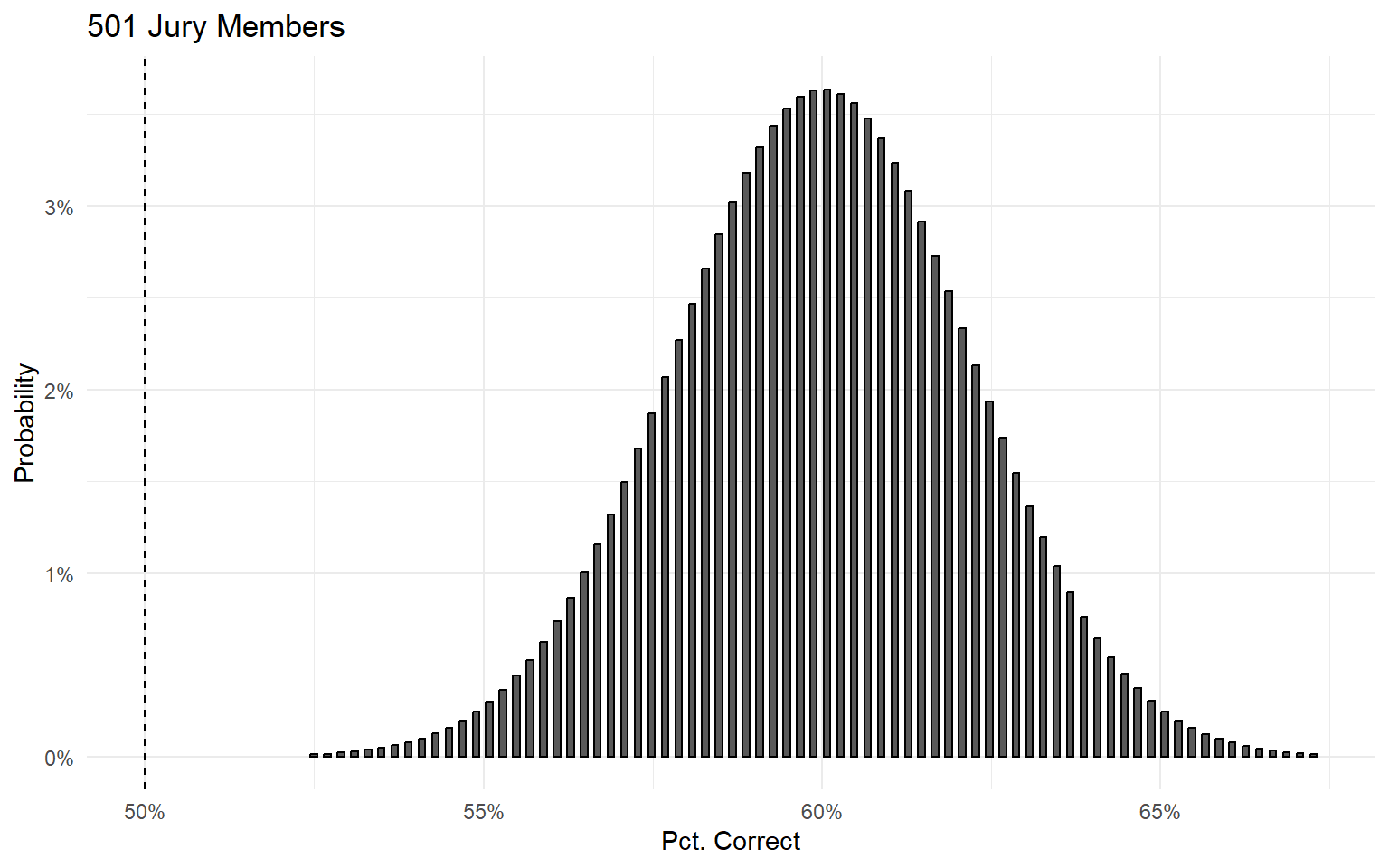
Condorcet Jury Theorem

• Majority rule is a powerful method for finding the right answer, if:

  • Individuals are competent \((p > \frac{1}{2})\).
  • Choices are made independently.
  • The group is large enough.

Wisdom of Crowds

• One last wrinkle: what if the decision being made isn’t binary (Yes/No)?

• What if the group is trying to make a decision about a continuous value?

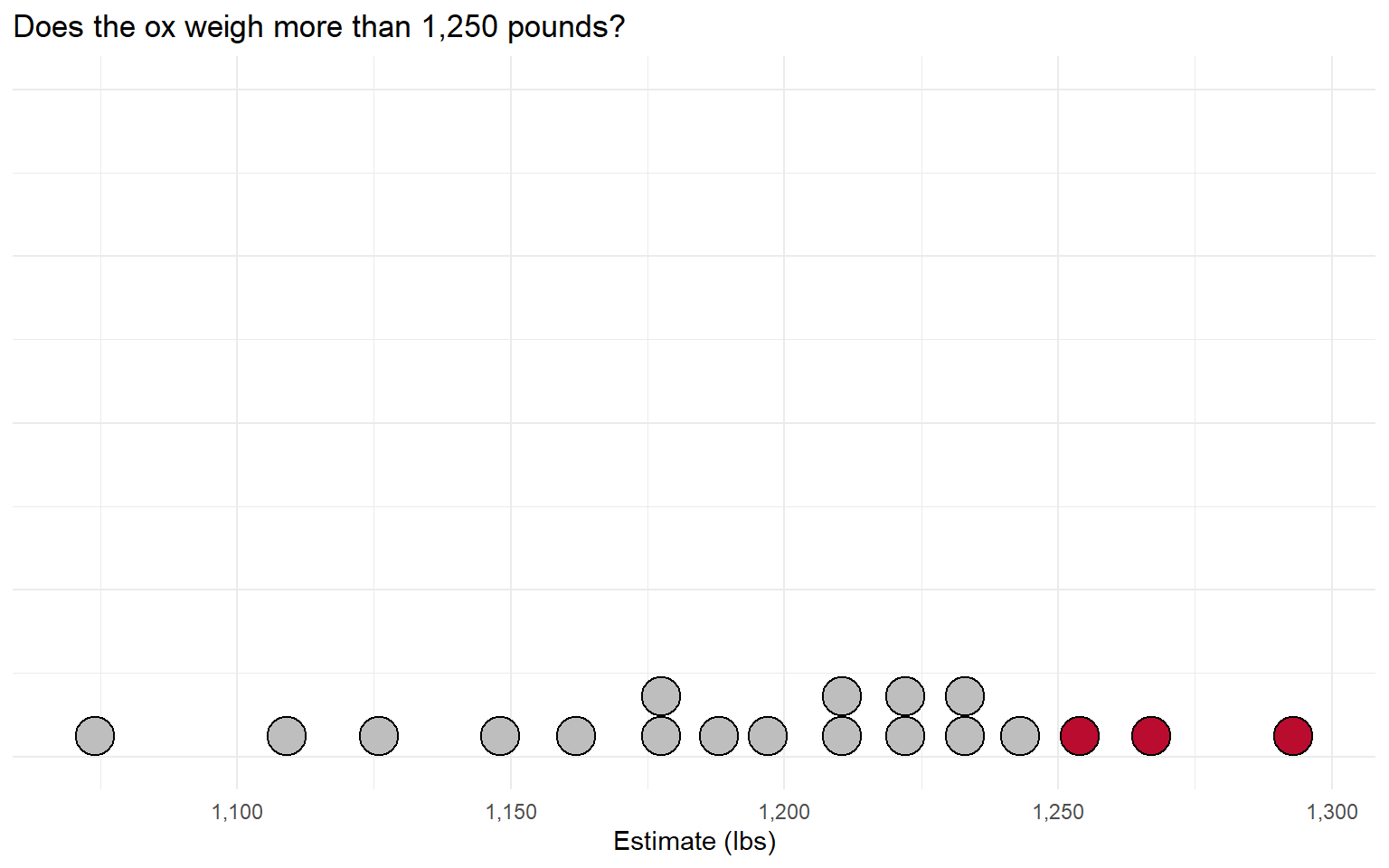
• Consider the ox weight-judging competition described in Tetlock Chapter 3.

• Participants paid sixpence to enter a competition to guess the weight of a “fat ox” (Galton 1907).

Wisdom of Crowds

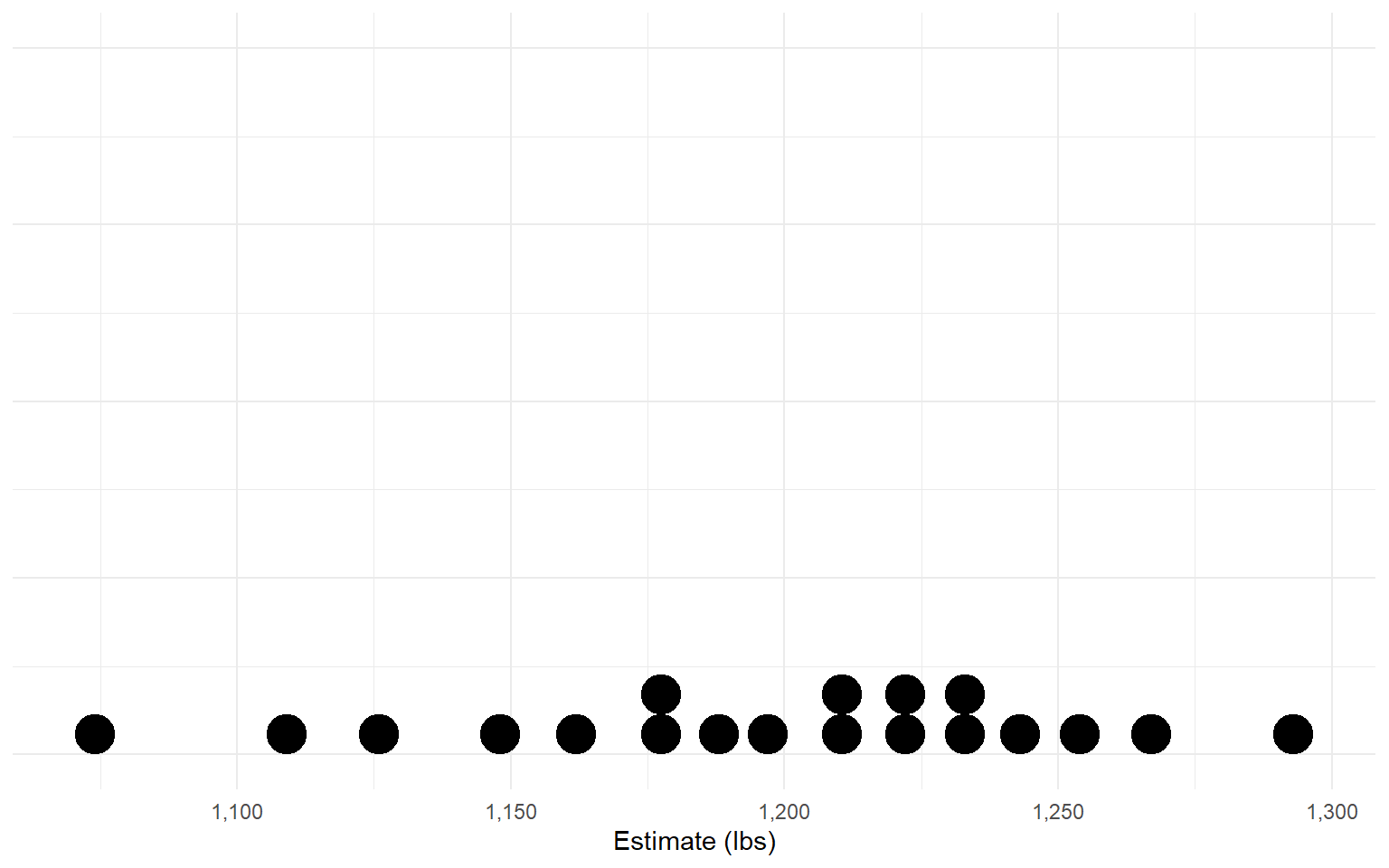
What is the “majority judgment” here?

Wisdom of Crowds

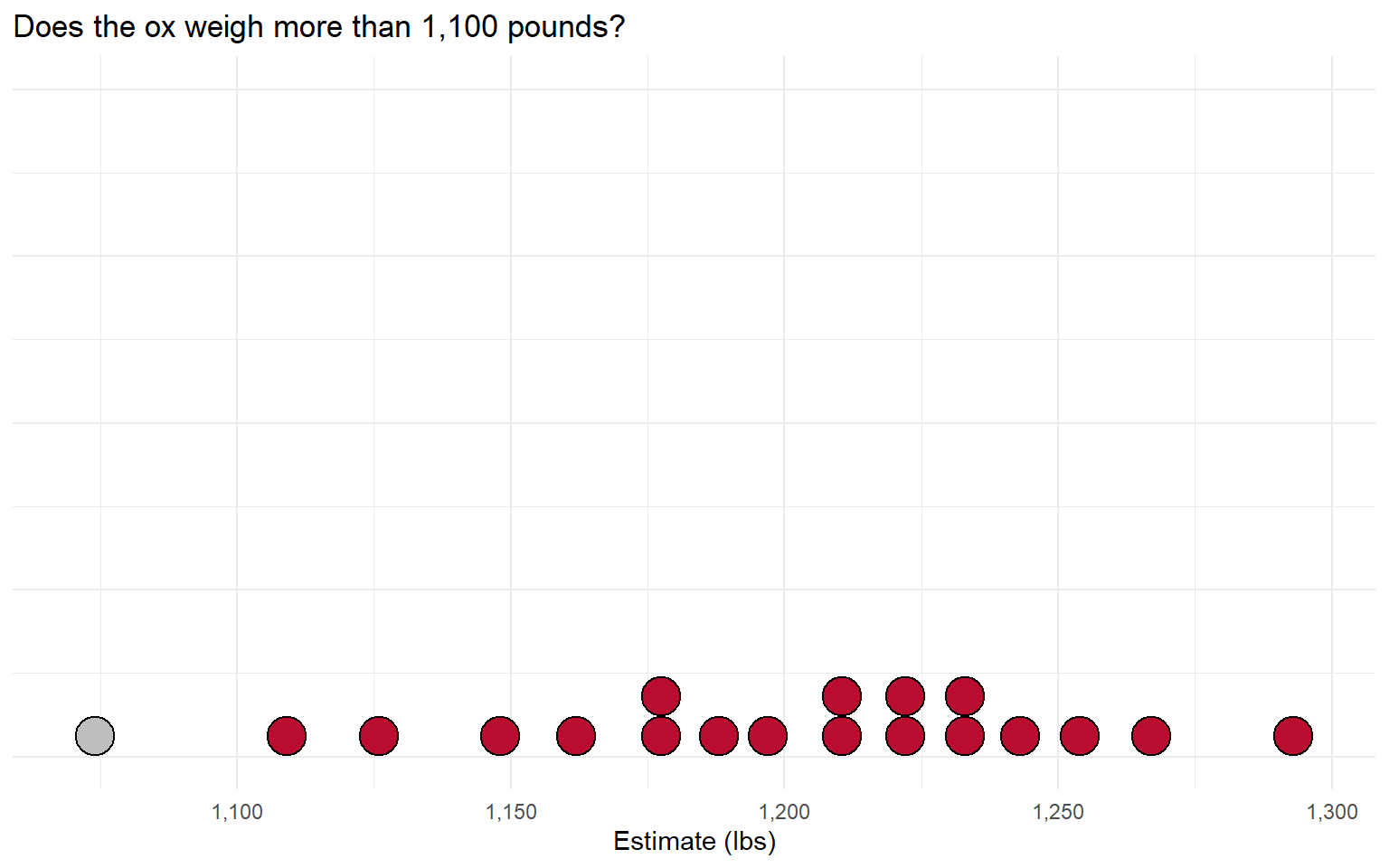
Imagine we broke this down into a series of binary (Yes/No) votes.

Wisdom of Crowds

If the majority says “it weighs more than that”, adjust the question higher:

Wisdom of Crowds

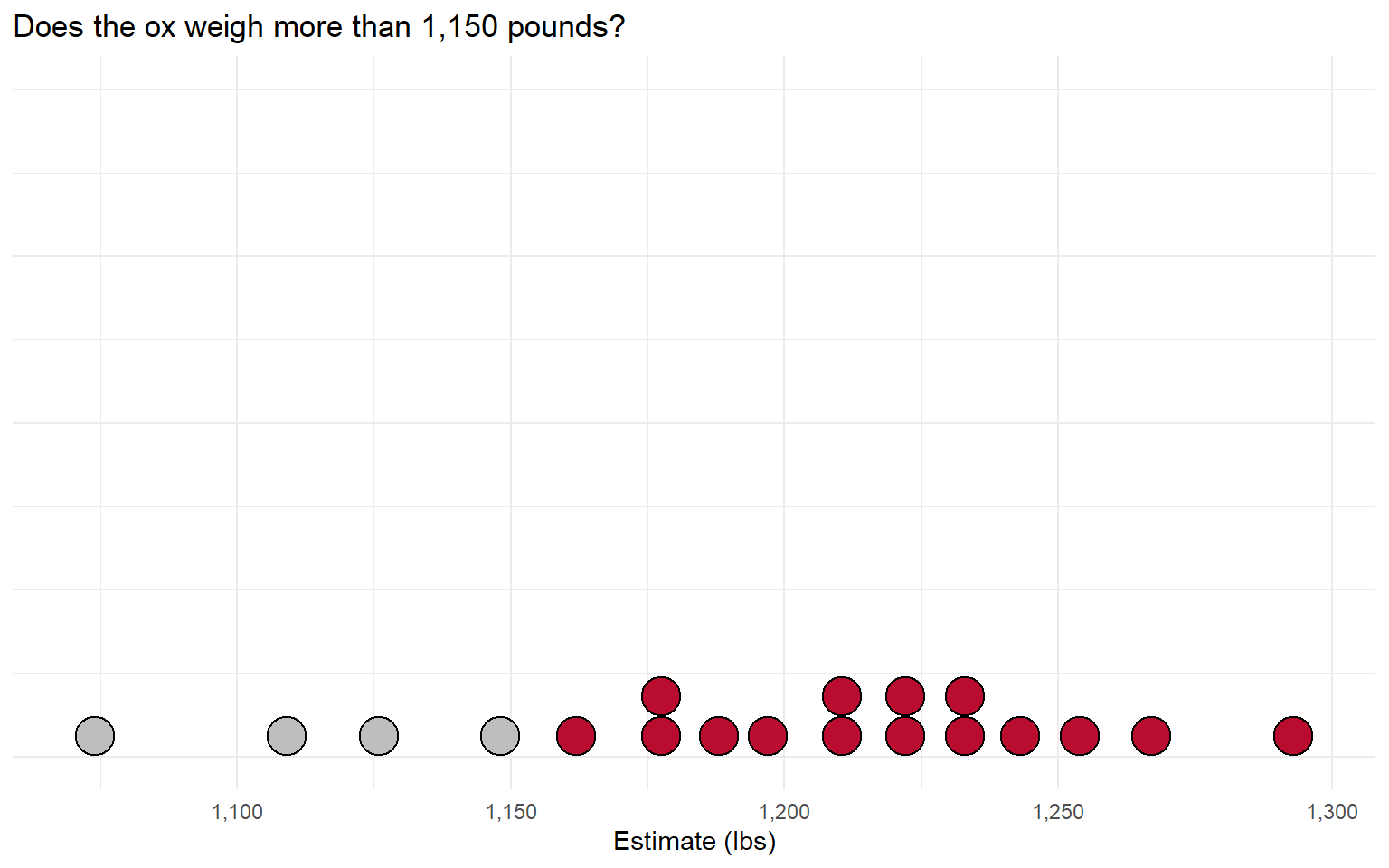
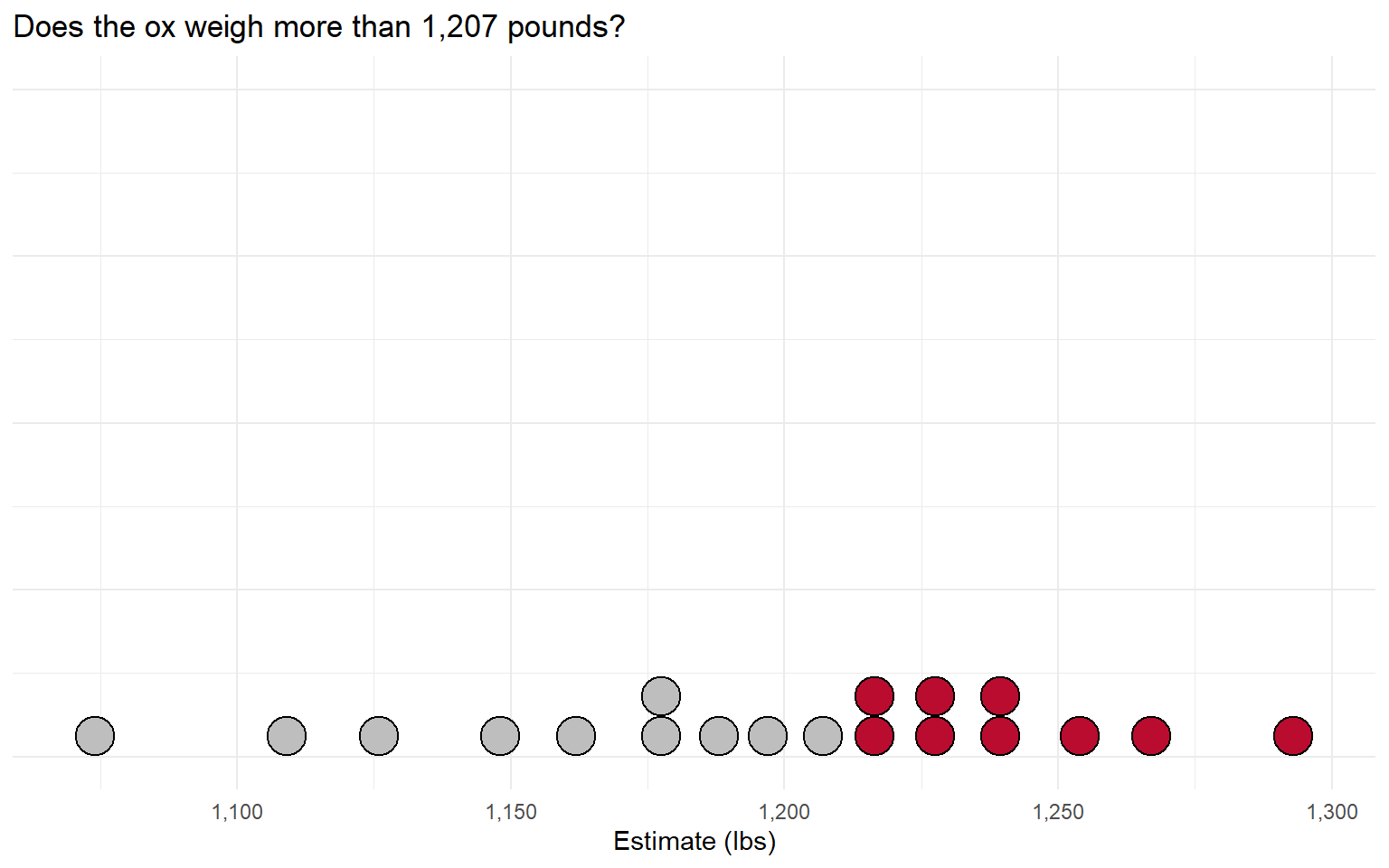
If the majority says “it weighs less than that”, adjust the question lower:

Wisdom of Crowds

This process will finally stop when we get to the median voter (Black 1948).

Wisdom of Crowds

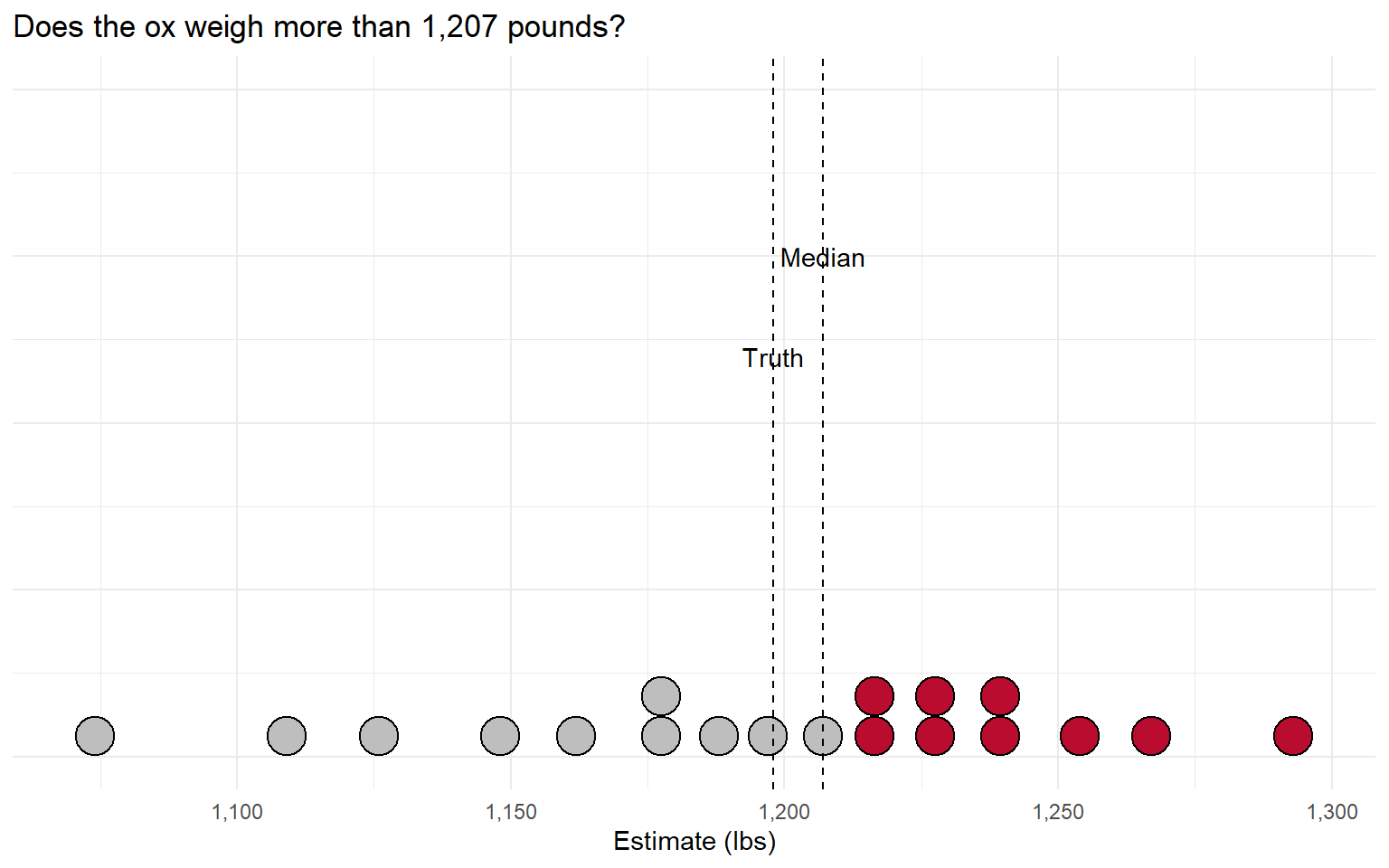
In Galton’s experiment, the median voter was off by only 9 pounds!

Median Voter Theorem

• The median voter theorem (Black 1948) says that the median is the only position that cannot be defeated by a majority vote.

• This follows from the definition of the median:

  • 50% of the group lies to the right.

  • 50% of the group lies to the left.

  • Any majority voting bloc (>50%) must include the median.

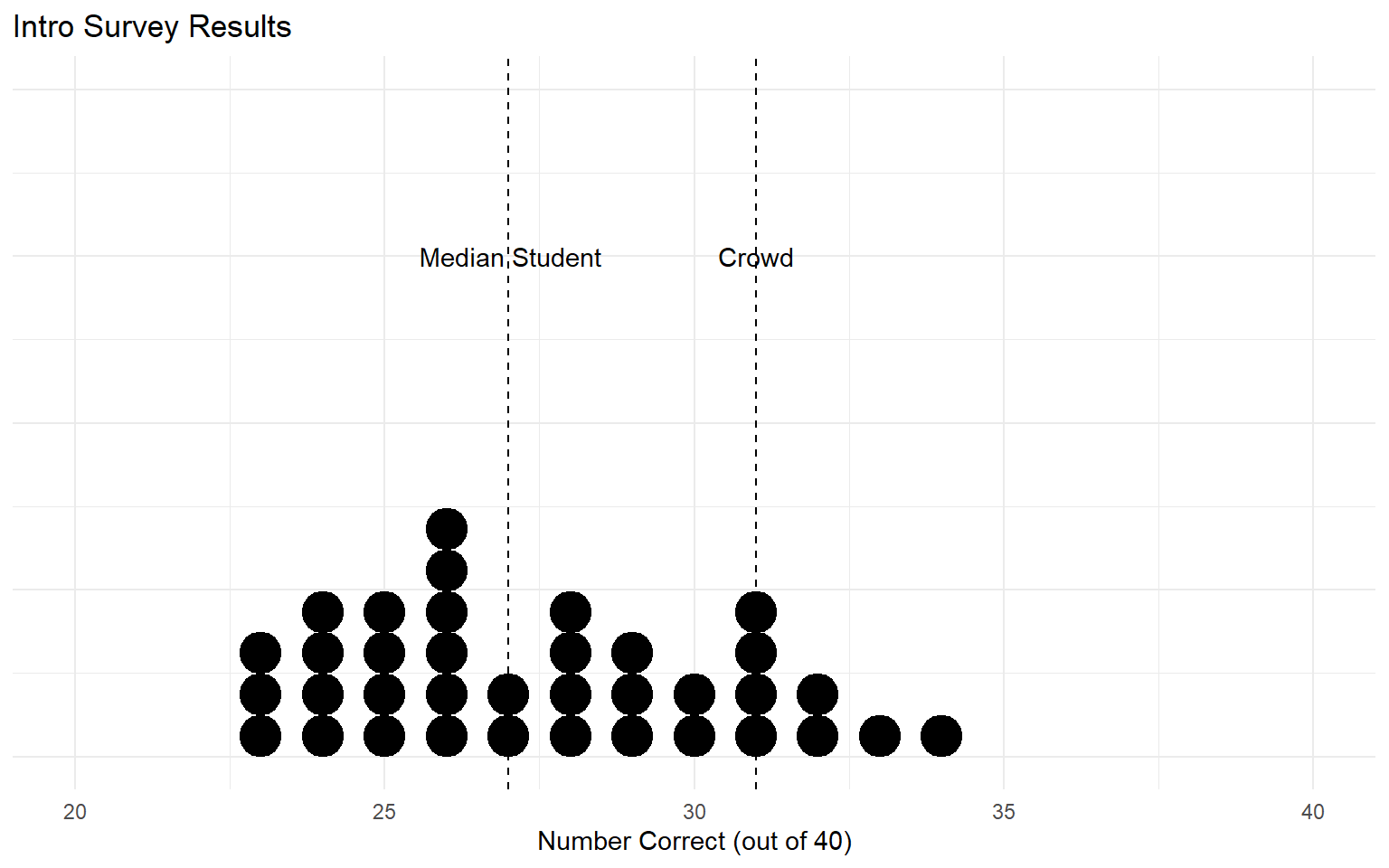
• So we can think of the “majority judgment” as the position of the median voter.

Takeaways

• The Condorcet Jury Theorem shows when we can expect majority rule to yield good judgments.

  • Individuals must be competent/independent, and you need a large group.

• The median voter theorem says that, when you’re making judgments on a continuous spectrum, majority = median.

  • This is why the “Crowd” point on our course website is the median forecast.

• Next Time: What to do when we don’t quite believe that independence assumption…

References

Black, Duncan. 1948. “On the Rationale of Group Decision-Making.” Journal of Political Economy 56 (1): 23–34. https://doi.org/10.1086/256633.

Galton, Francis. 1907. “Vox Populi.” Nature 75 (1949): 450–51. https://doi.org/10.1038/075450a0.