Long Tails
POLS 3220: How to Predict the Future
Today’s Agenda
- Review the Central Limit Theorem (CLT)
- Describe the problem of tail risk
- Consider when the assumptions of CLT may be violated
- Introduce long tail probability distributions
Warmup

Using the definition of the Central Limit Theorem, explain why the Galton Board produces a bell curve shape.
Tail Risk
A common forecasting problem is to try to quantify “tail risk”. What’s the probability of an extreme result, far outside what we ordinarily expect?
Last time, we discussed the margin of error, which is a measure of tail risk in political polling.
But this type of problem crops up everywhere: financial analysis, military planning, emergency management, etc.
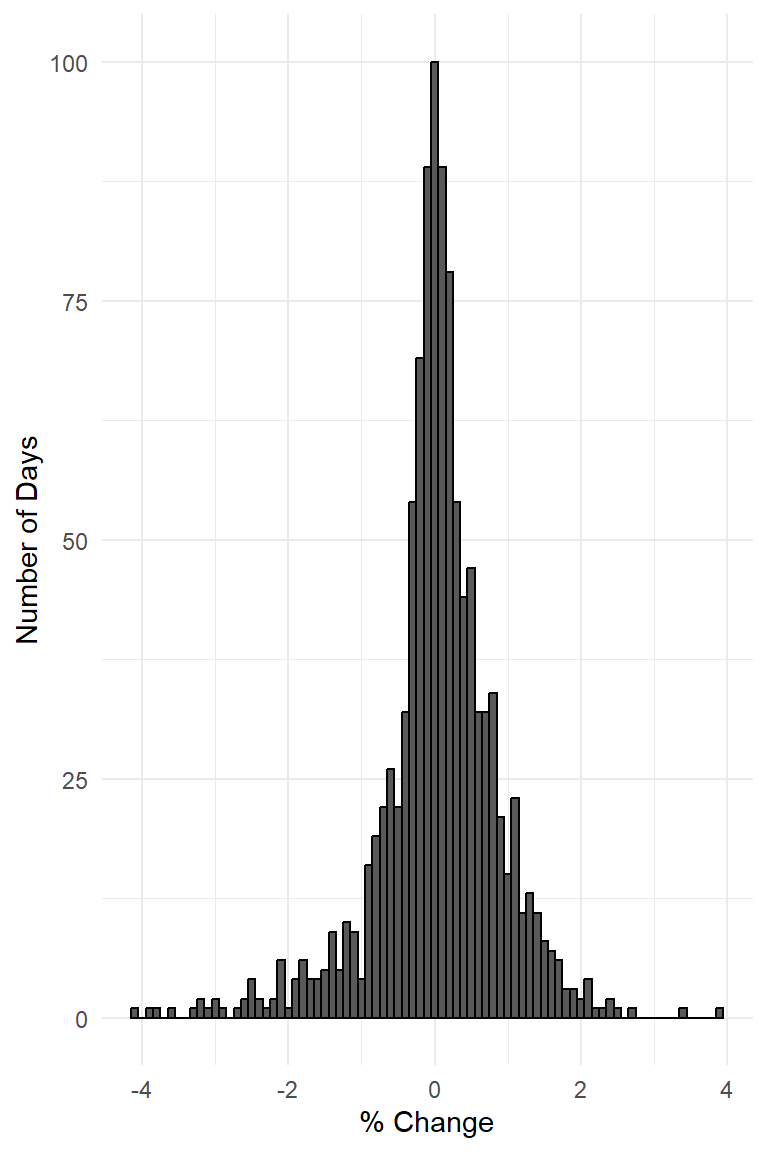
Bell Curves Have Low Tail Risk
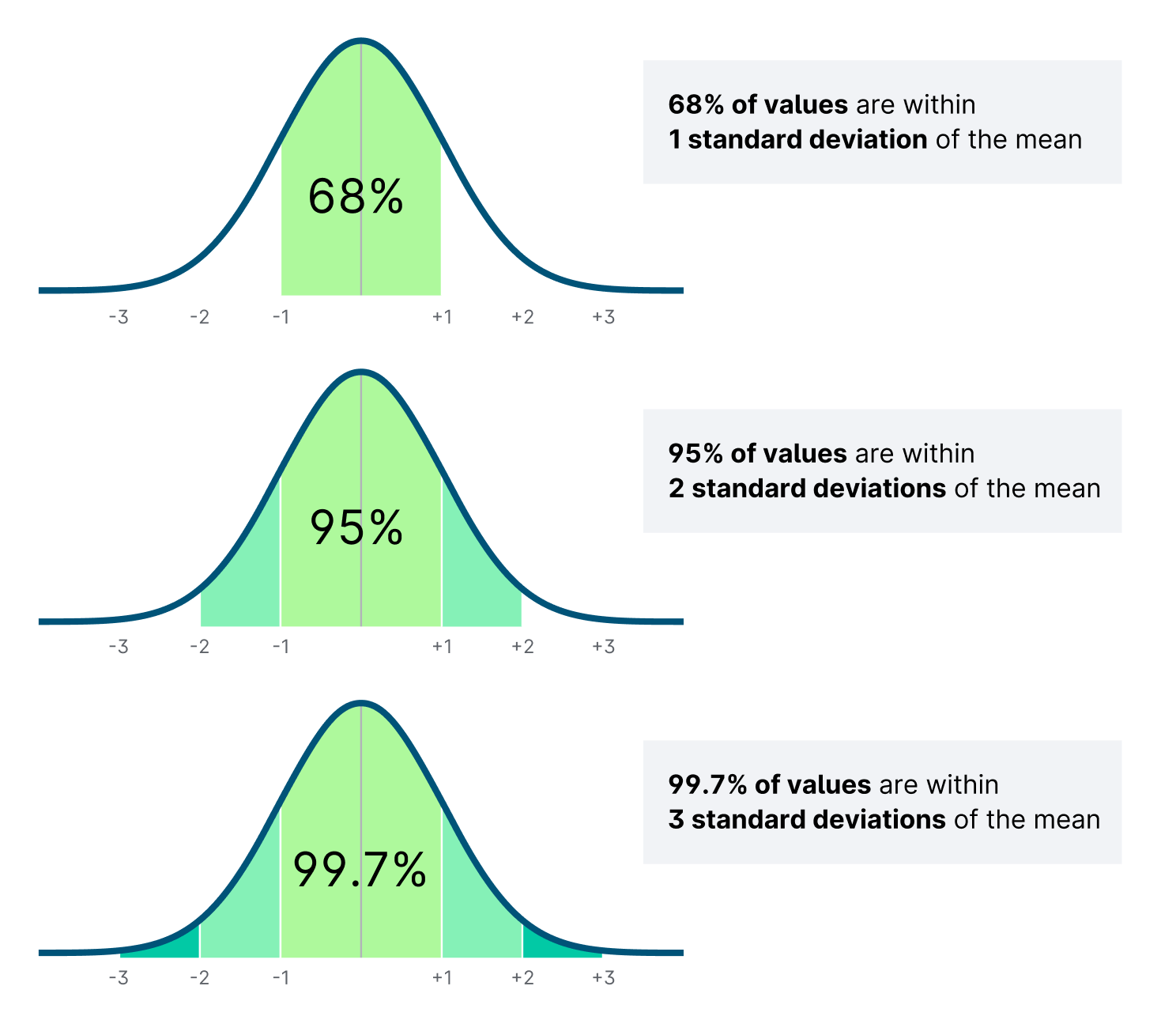
- Standard deviation \((\sigma)\) is a measure of the spread of the distribution. It measures how far, on average, observations lie from their expected value.
- A “2 sigma” event should happen only 5% of the time.
- A “3 sigma” event should happen only 0.3% of the time.
Financial Markets Example
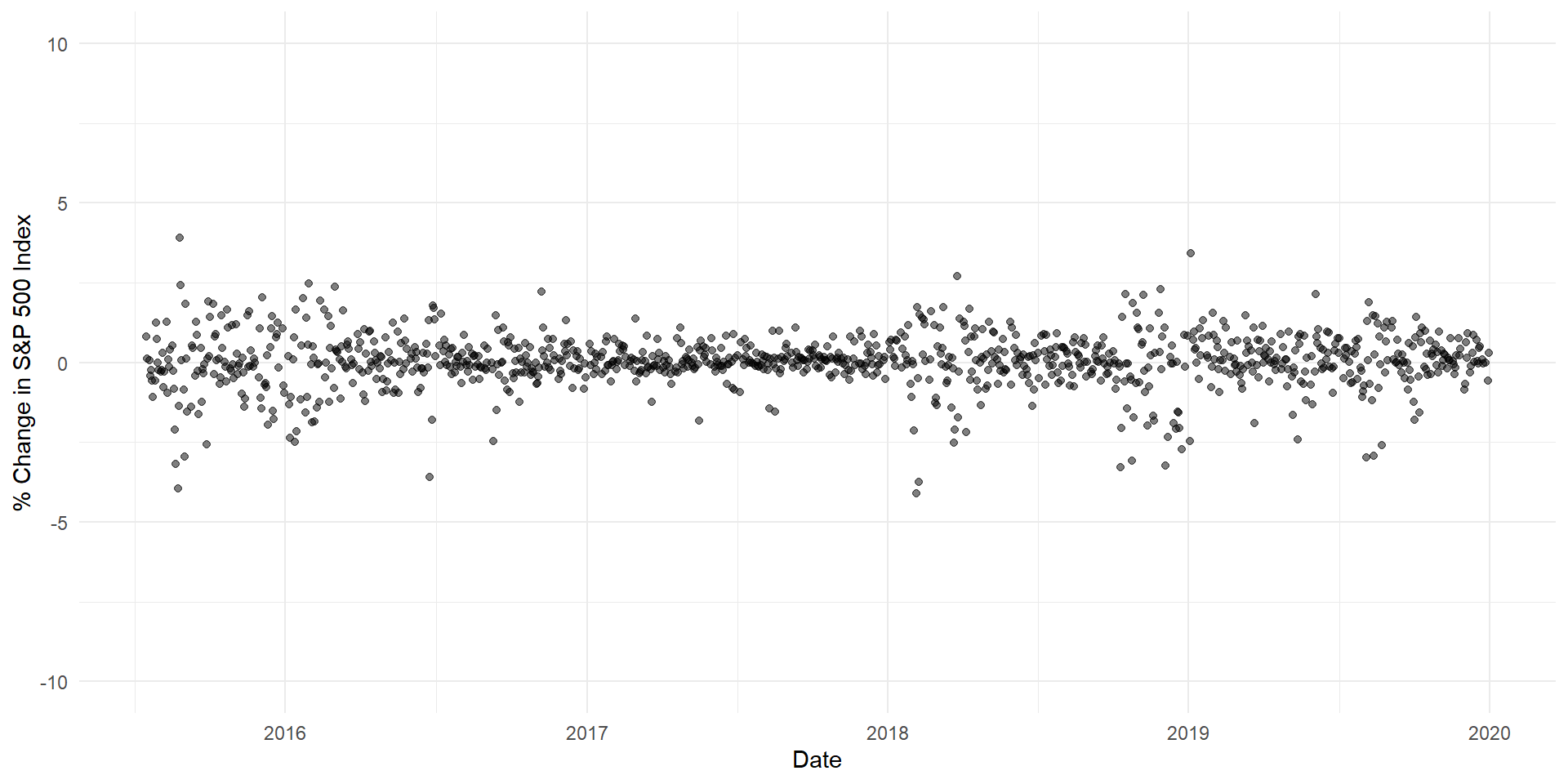
Financial Markets Example
It…looks like a bell curve?
\(\sigma =\) 0.84
So we should expect price movements greater than 1.68% only on about 1 in every 20 trading days.
And that’s basically true! On 94% of trading days, price movements are within that range.
So what’s the problem?
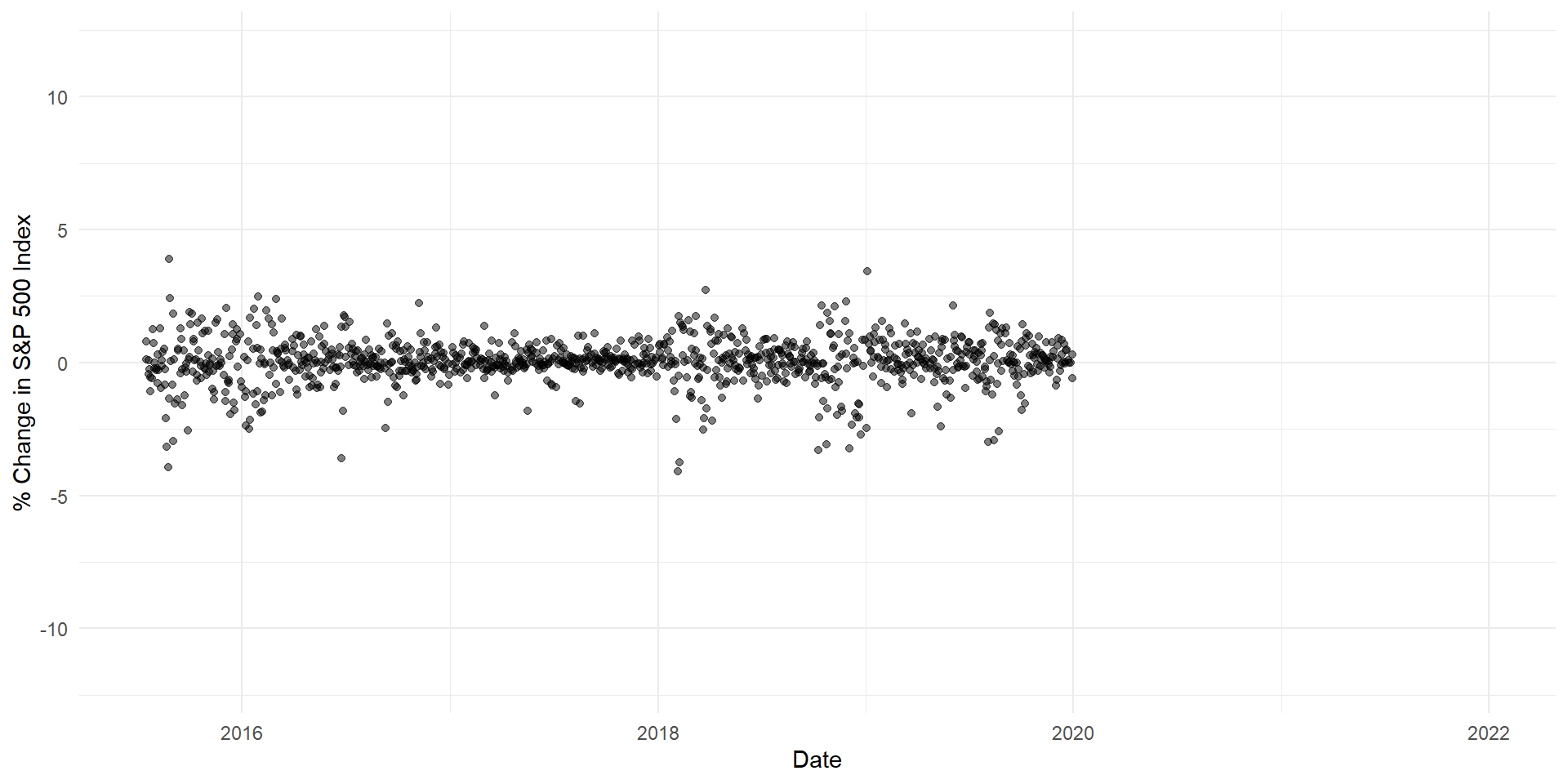
So what’s the problem?
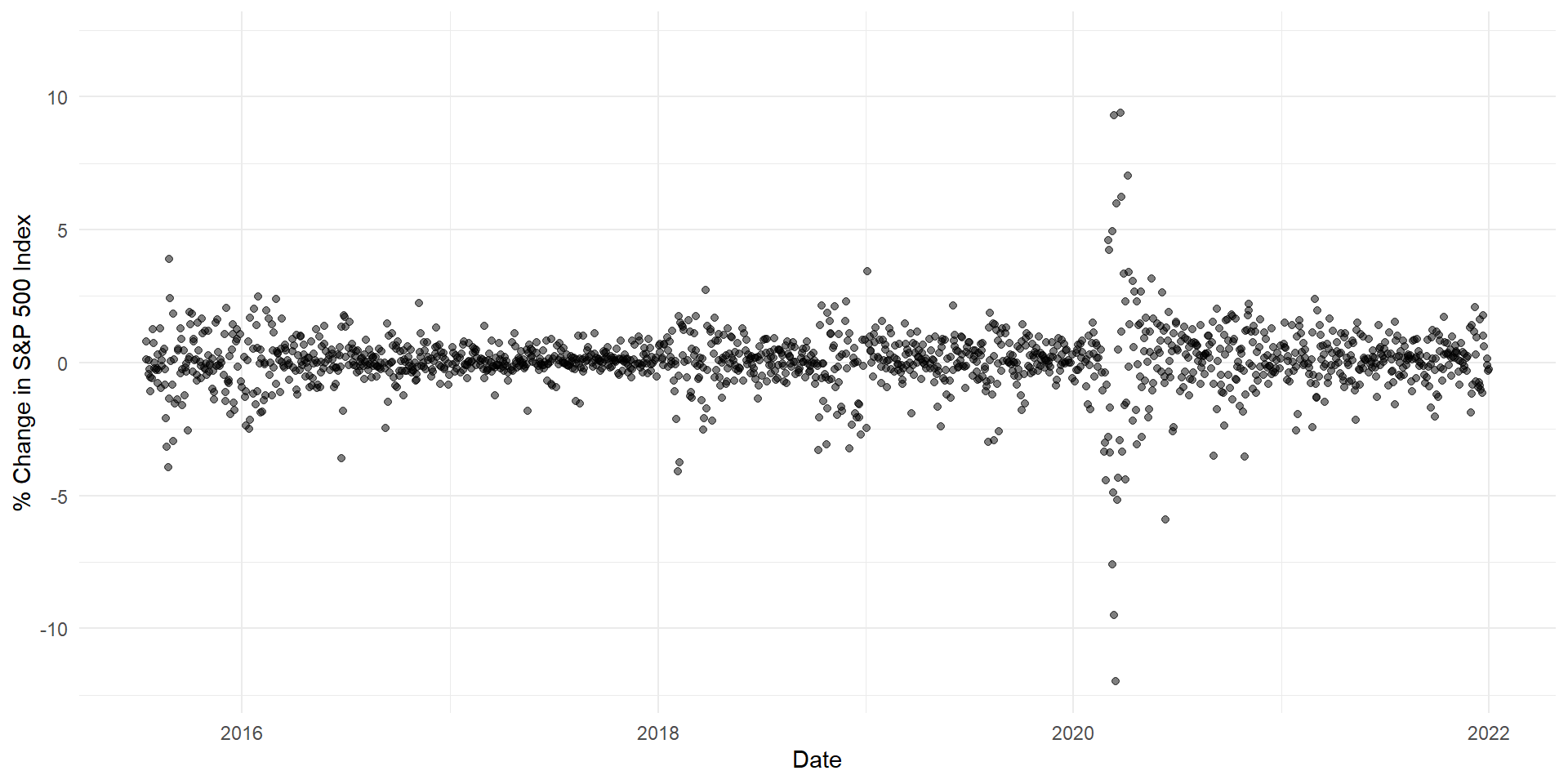
Long Tails
On March 16, 2020 the S&P 500 index dropped 11.98%.
This was a “14 sigma” event.
The probability of such an event, according to the standard bell curve, is approximately 0.0000000000000000000000000000000000000000007793537%.
To express that somewhat dramatically: if the New York Stock Exchange had operated every single day since the birth of the universe 13.8 billion years ago, we still wouldn’t expect to see a price movement that large.
Long Tails
So, financial markets are clearly have greater tail risk than a bell curve would expect (Taleb 2007).
Discuss: Why do you think that is? Which part of the Central Limit Theorem is violated here?
In the rest of the lecture, we’ll discuss two types of violations, and the long tail distributions they generate.
Violation 1: Multiplicative Processes
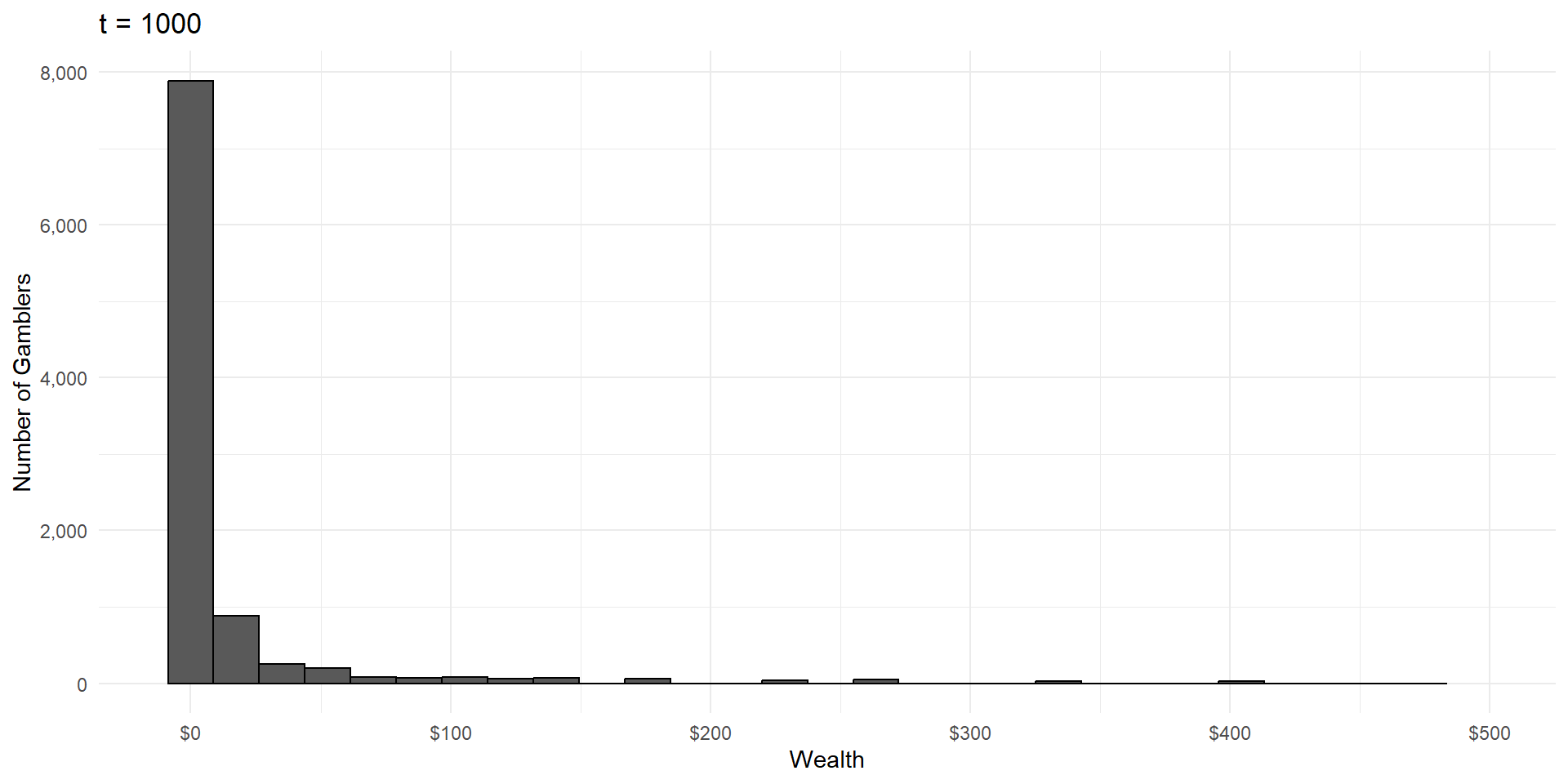
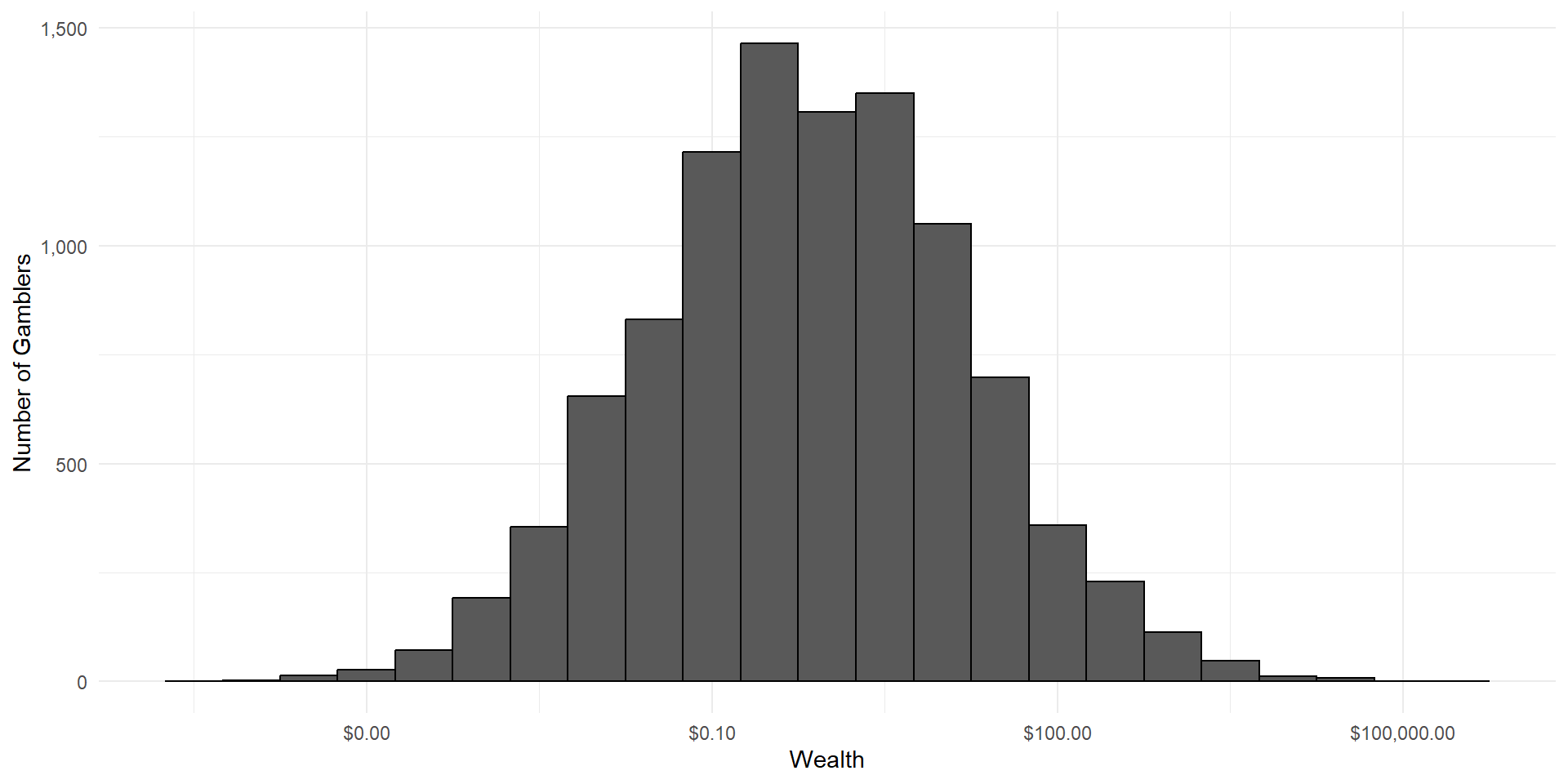
Imagine a group of gamblers who each start with $100.
They all make a series of wagers that either cause them to win or lose 10% of their money, with equal probability.
What will the wealth distribution look like after a large number of these gambles?
As in CLT, wealth is the result of a large number of independent random events.
But wealth is the product of these events, not the sum.
Violation 1: Multiplicative Processes
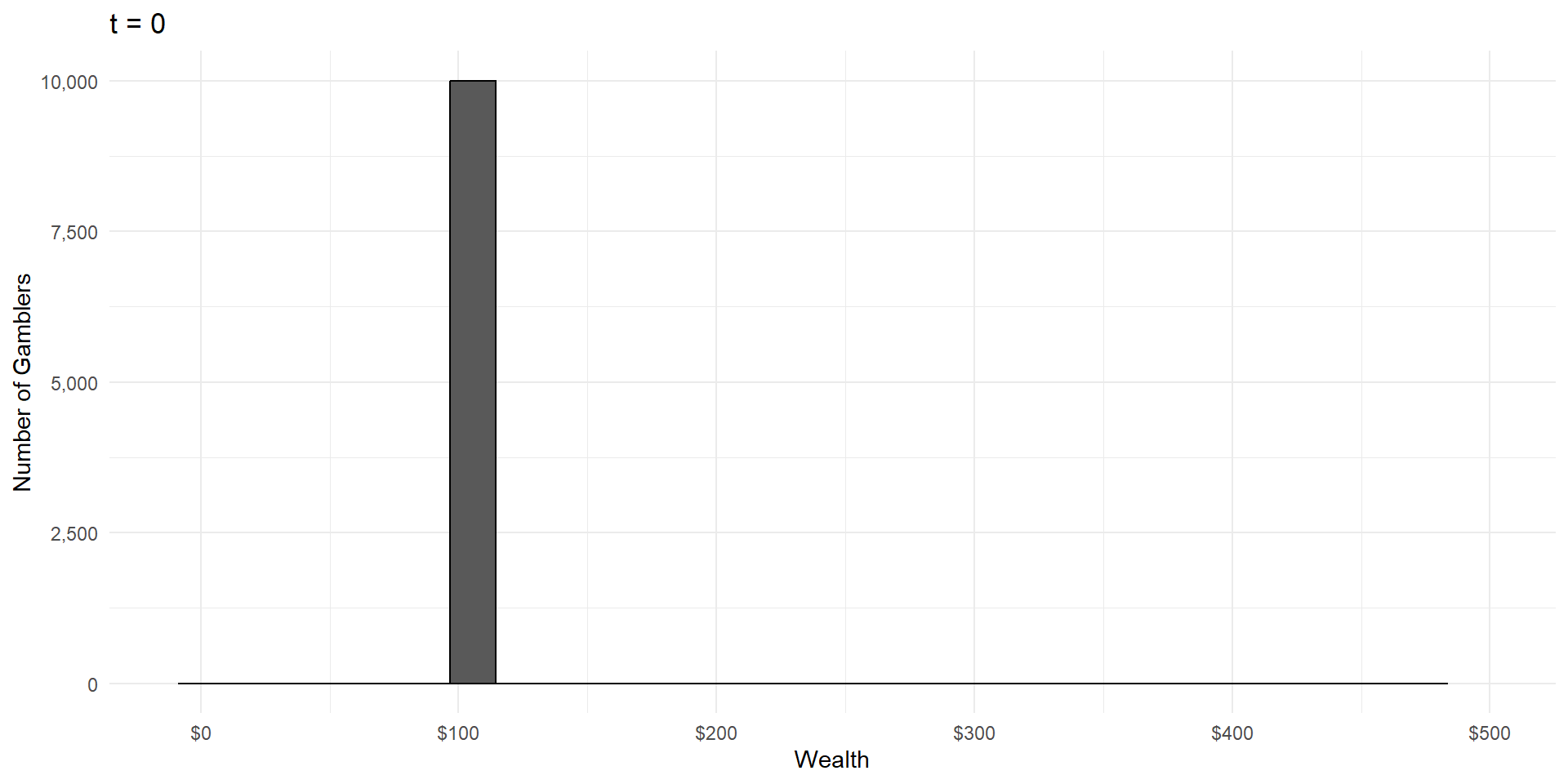
Violation 1: Multiplicative Processes
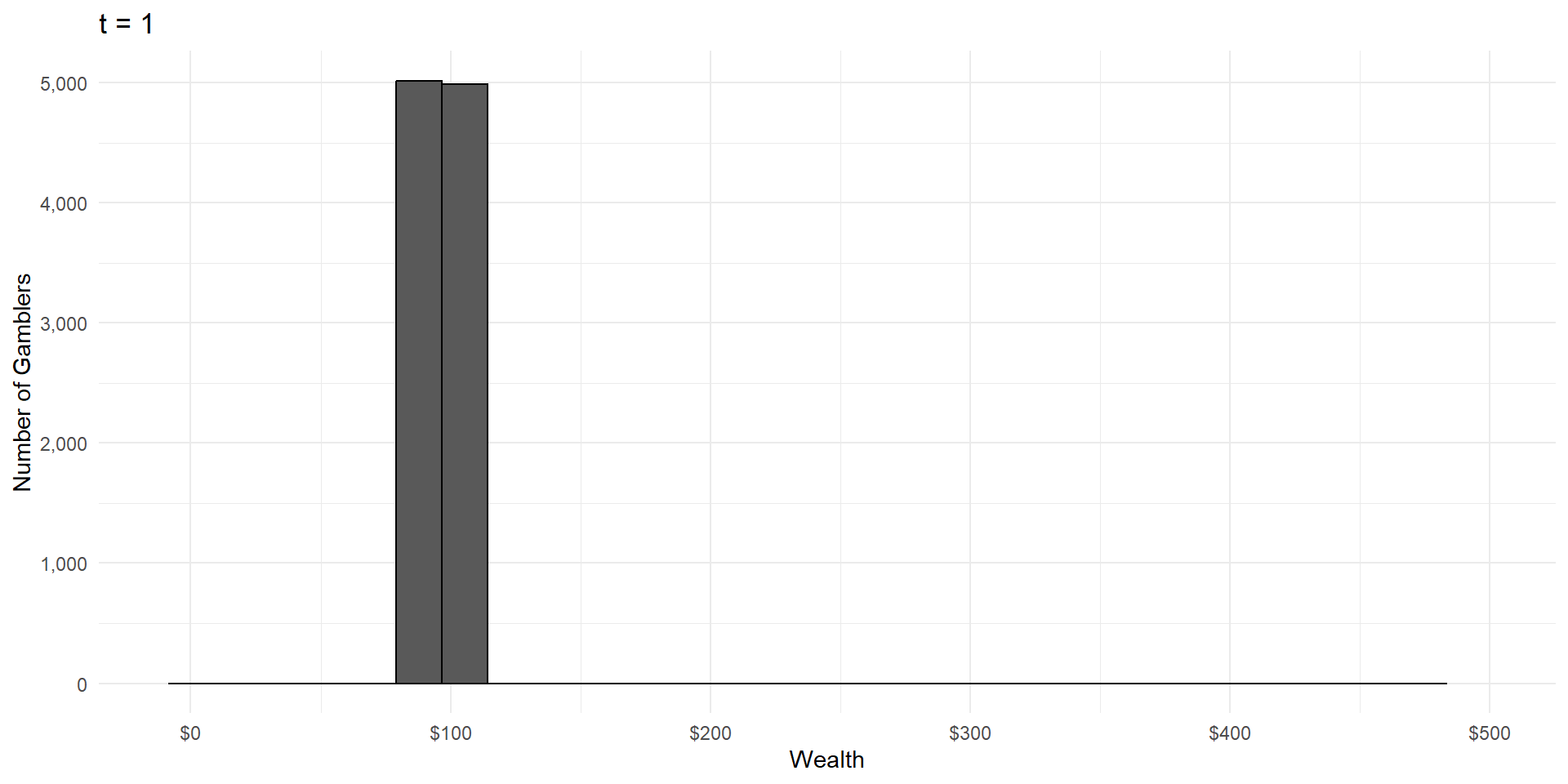
Violation 1: Multiplicative Processes
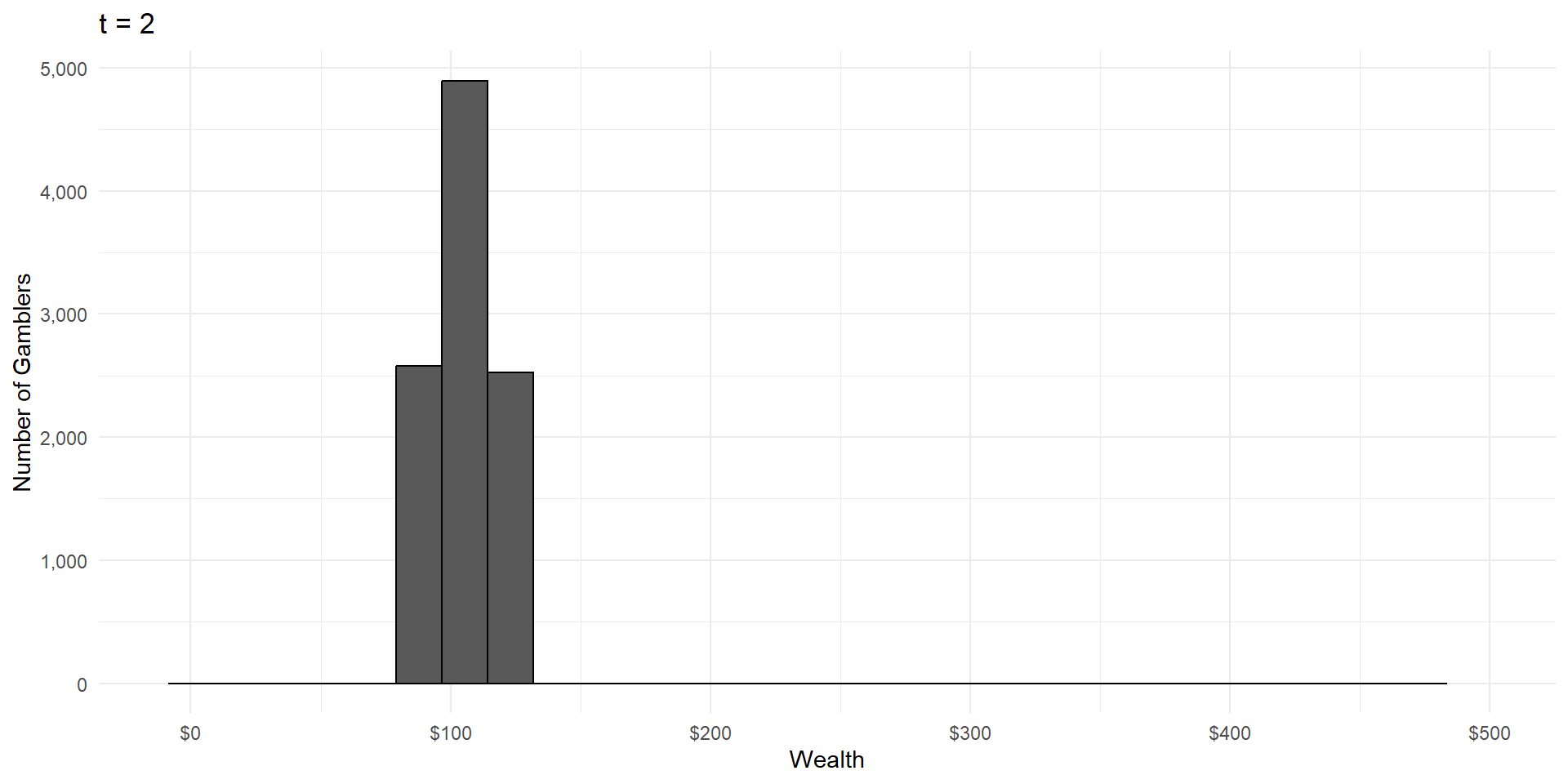
Violation 1: Multiplicative Processes
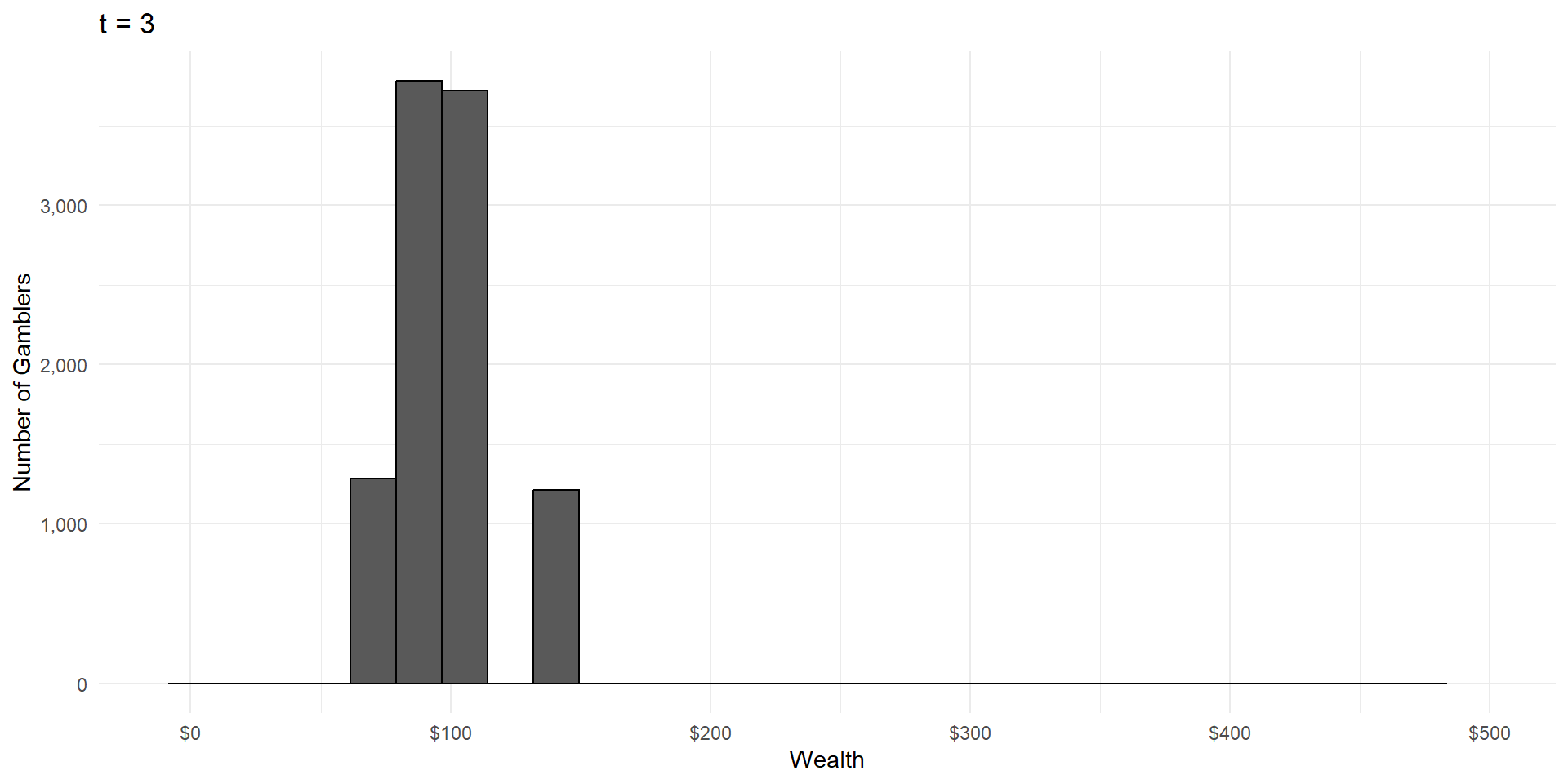
Violation 1: Multiplicative Processes
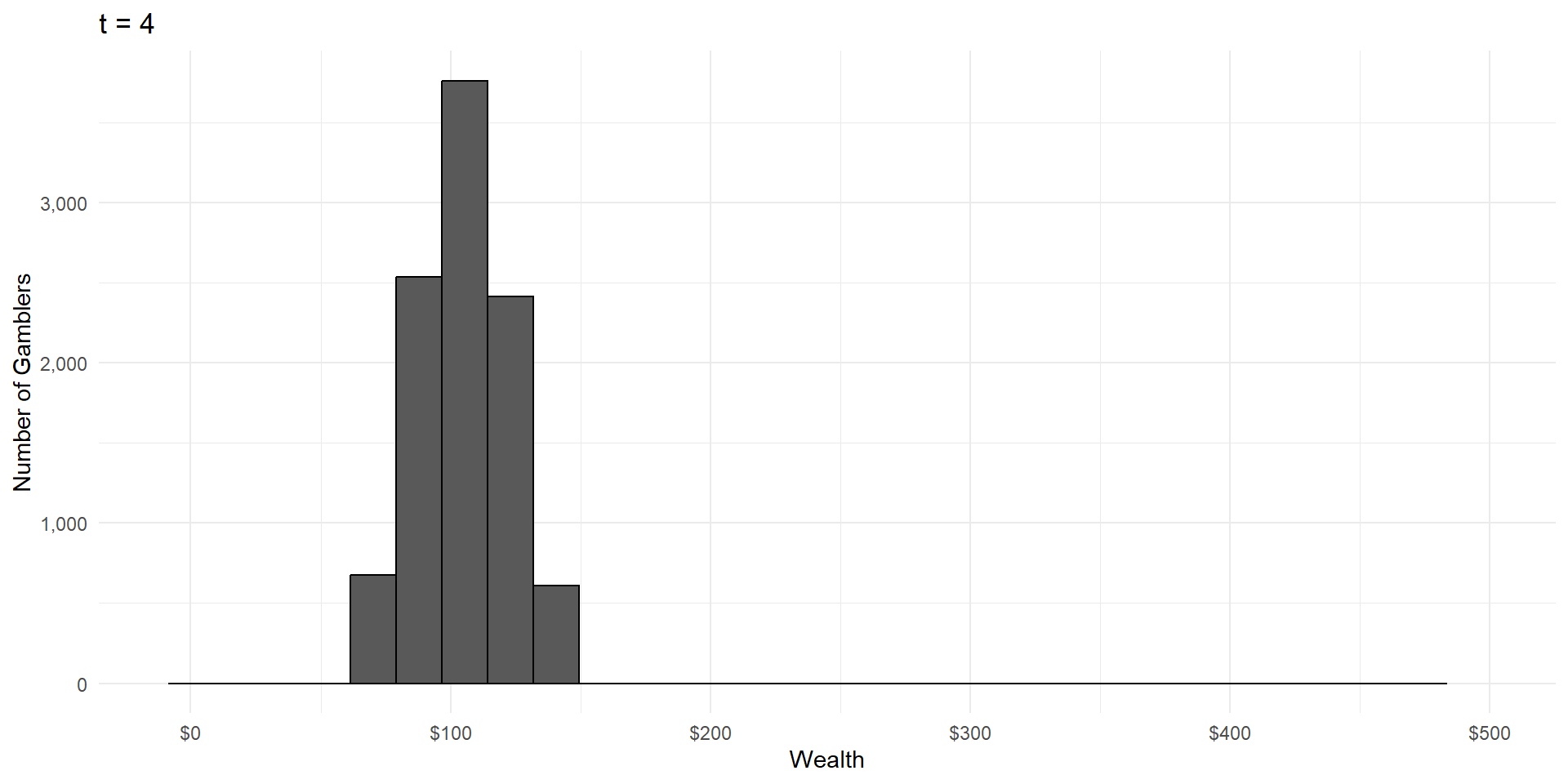
Violation 1: Multiplicative Processes
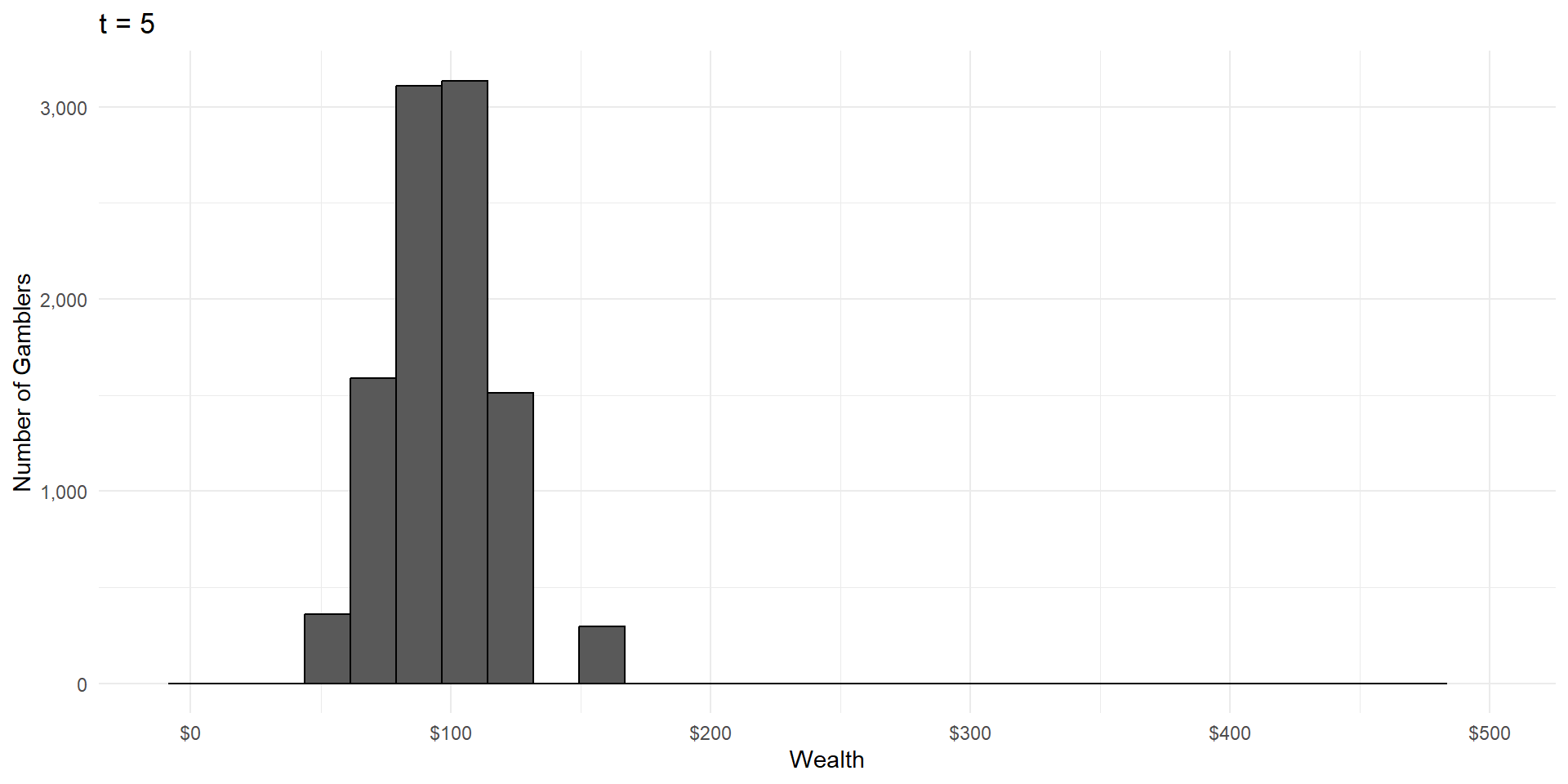
Violation 1: Multiplicative Processes
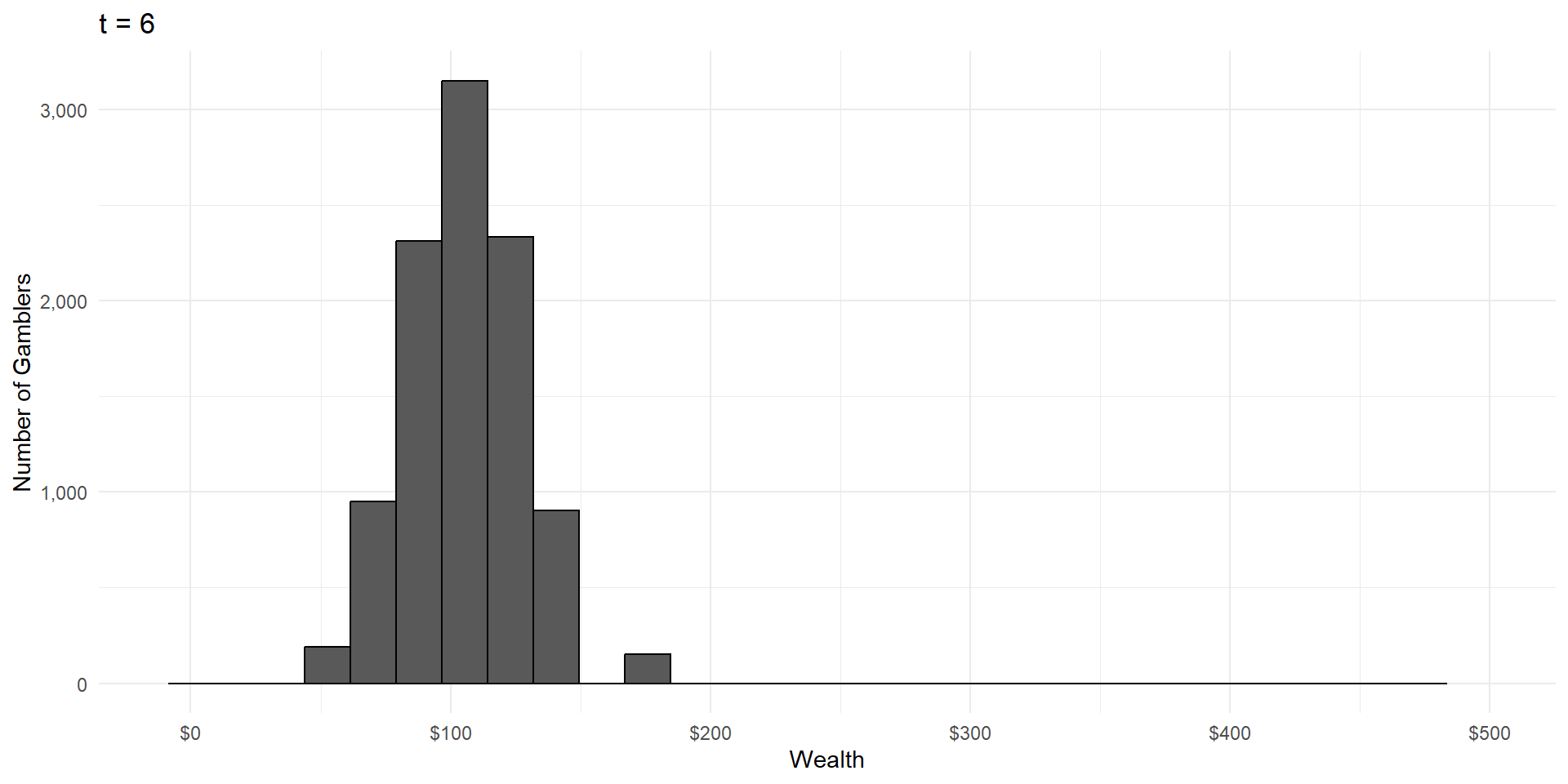
Violation 1: Multiplicative Processes
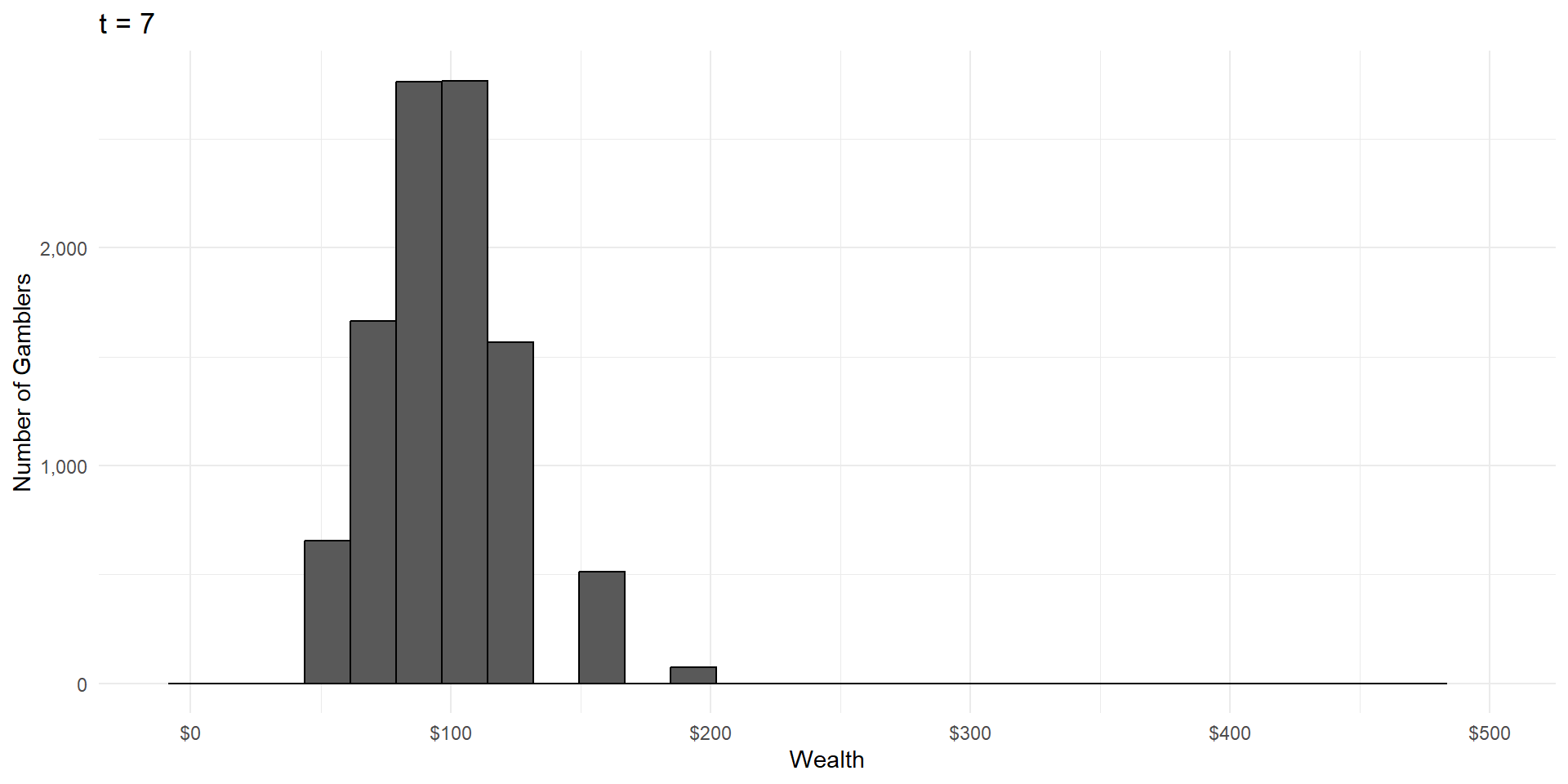
Violation 1: Multiplicative Processes
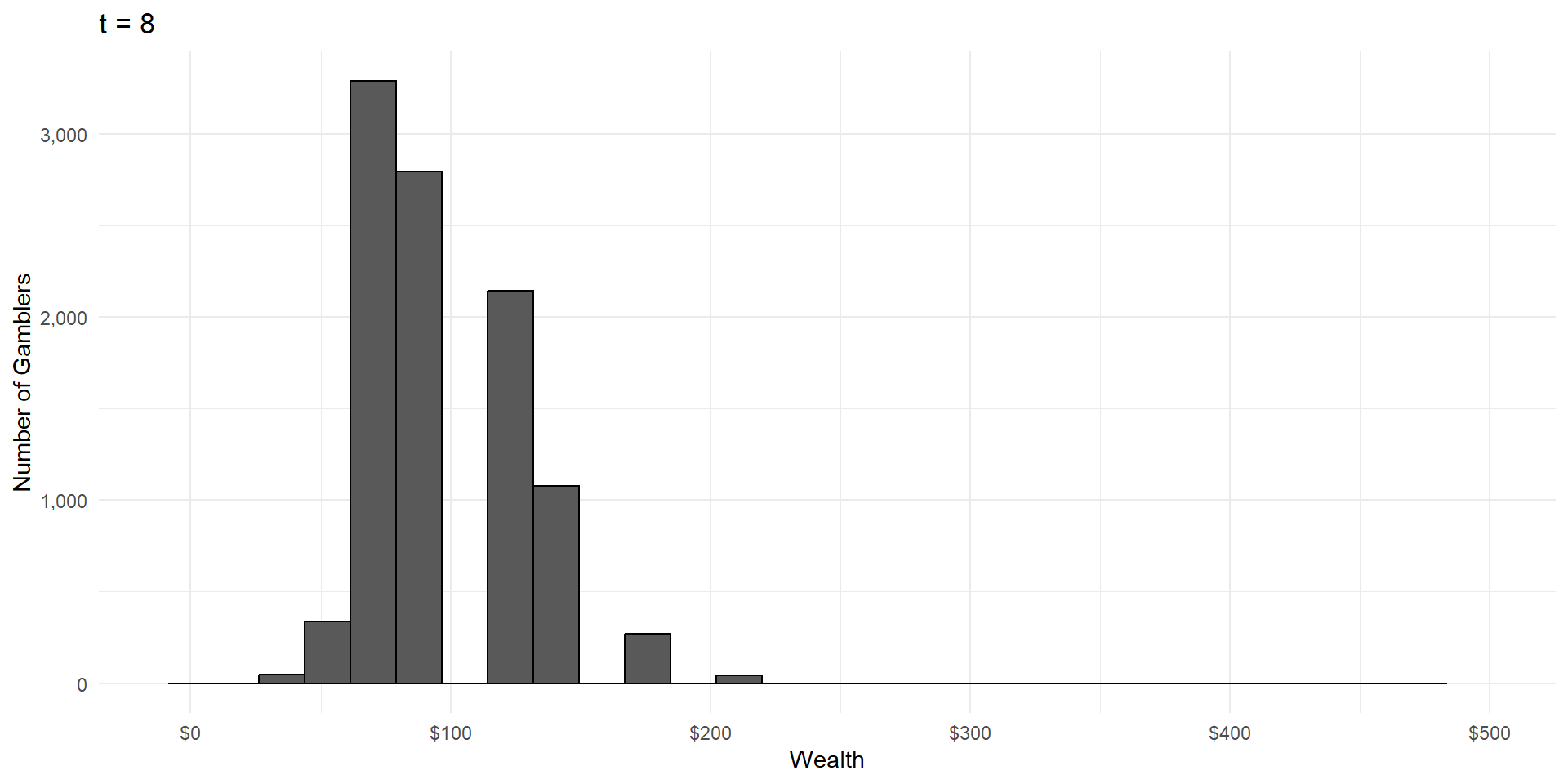
Violation 1: Multiplicative Processes
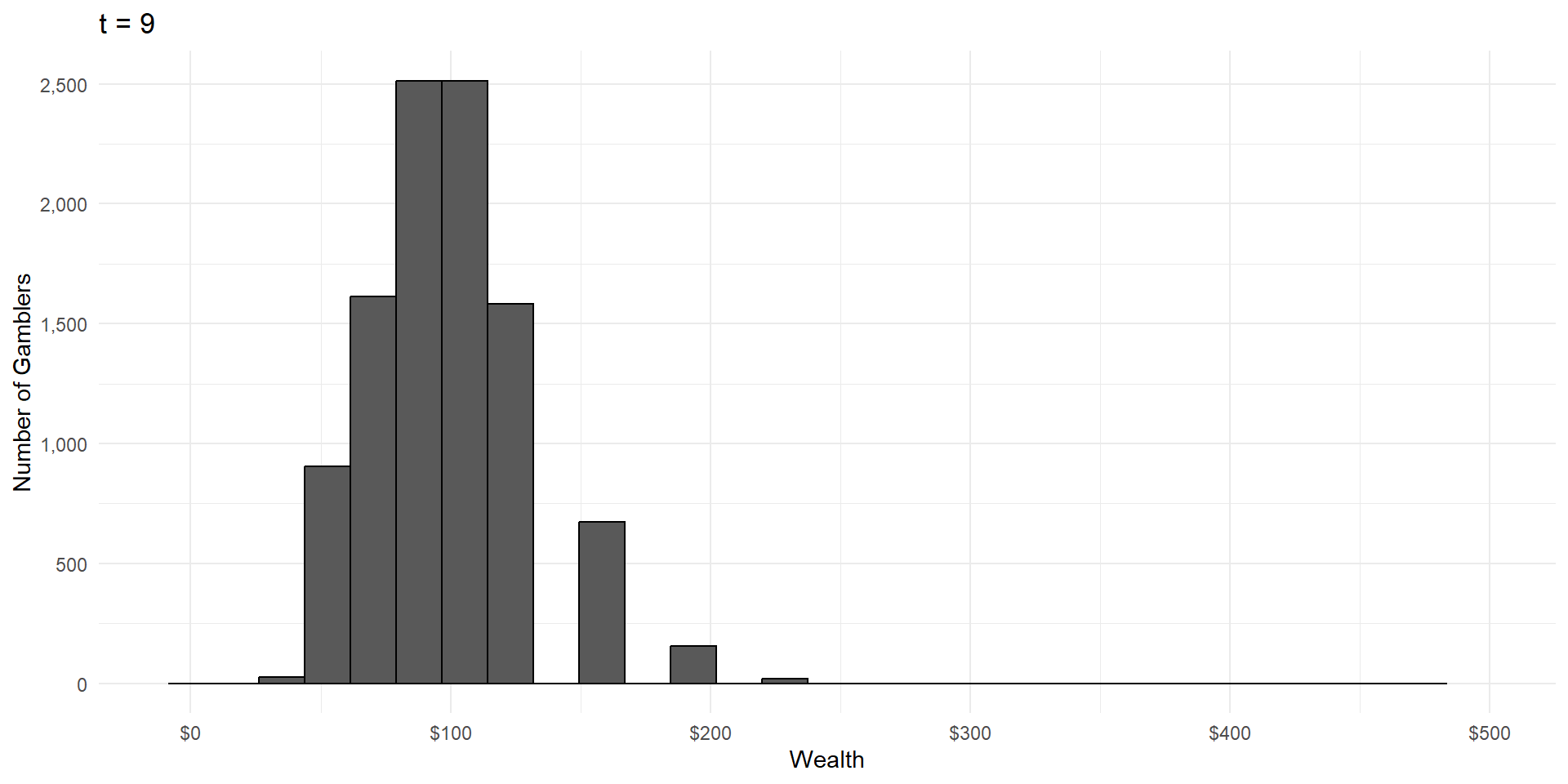
Violation 1: Multiplicative Processes
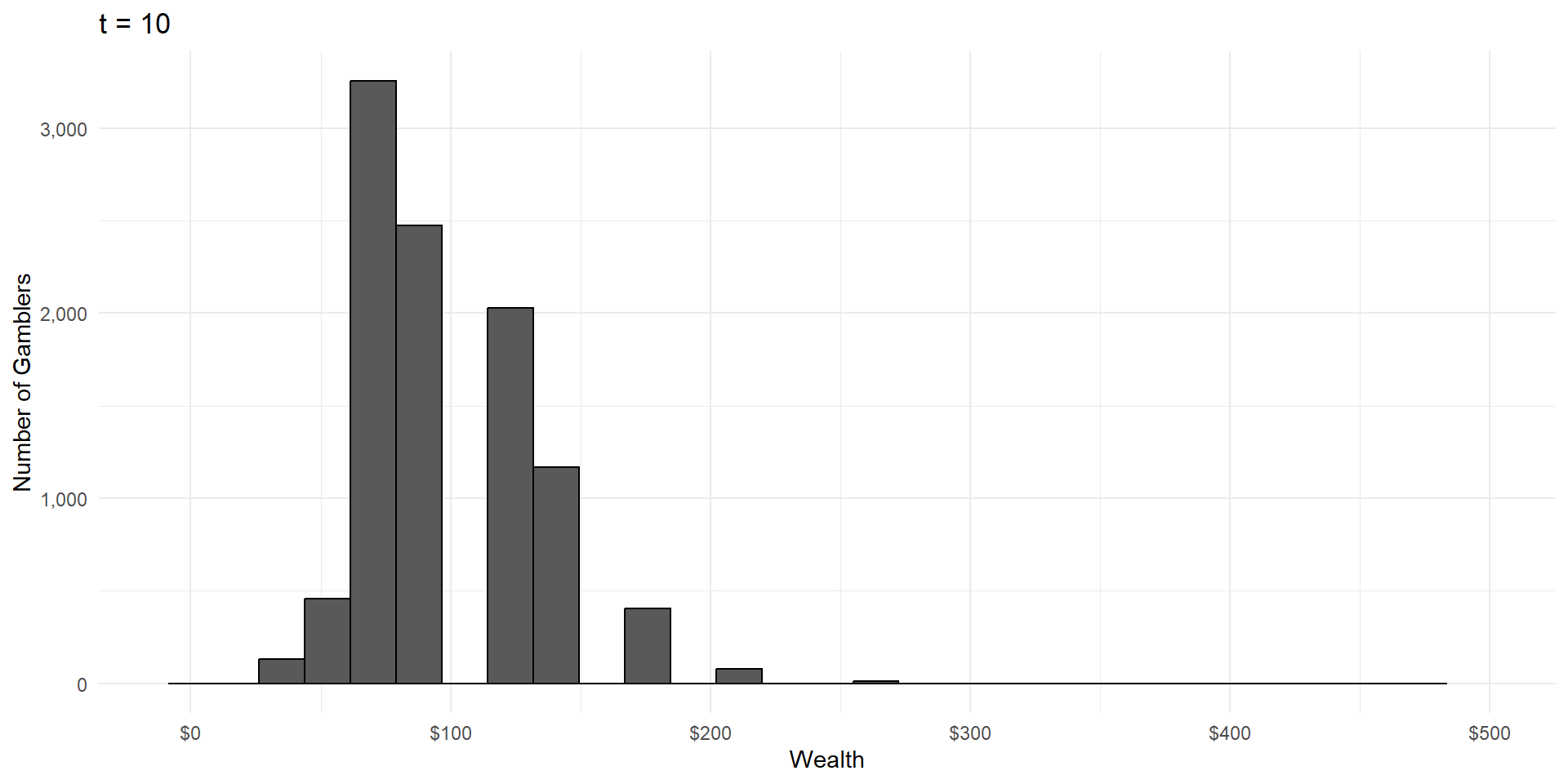
Violation 1: Multiplicative Processes
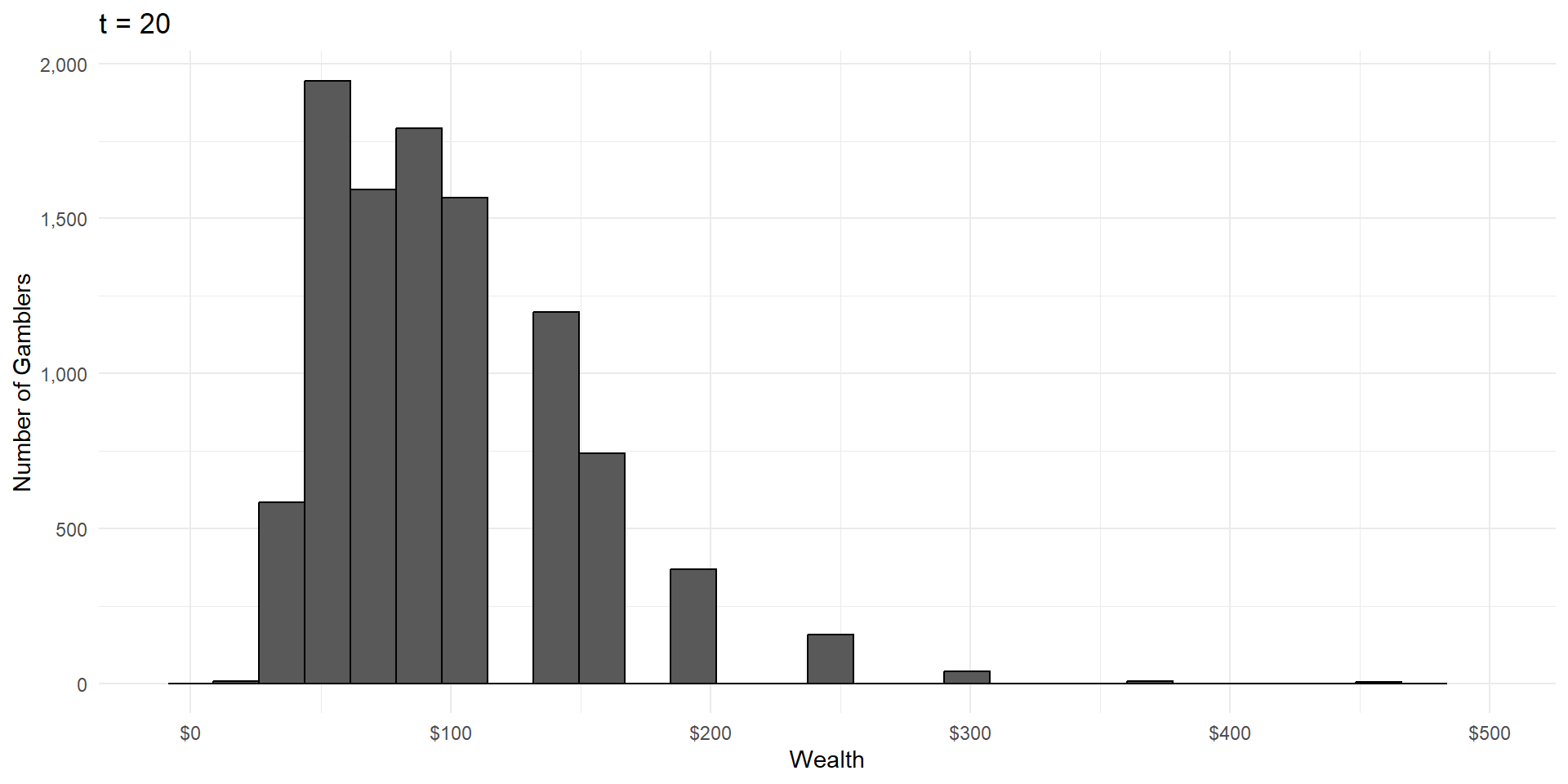
Violation 1: Multiplicative Processes
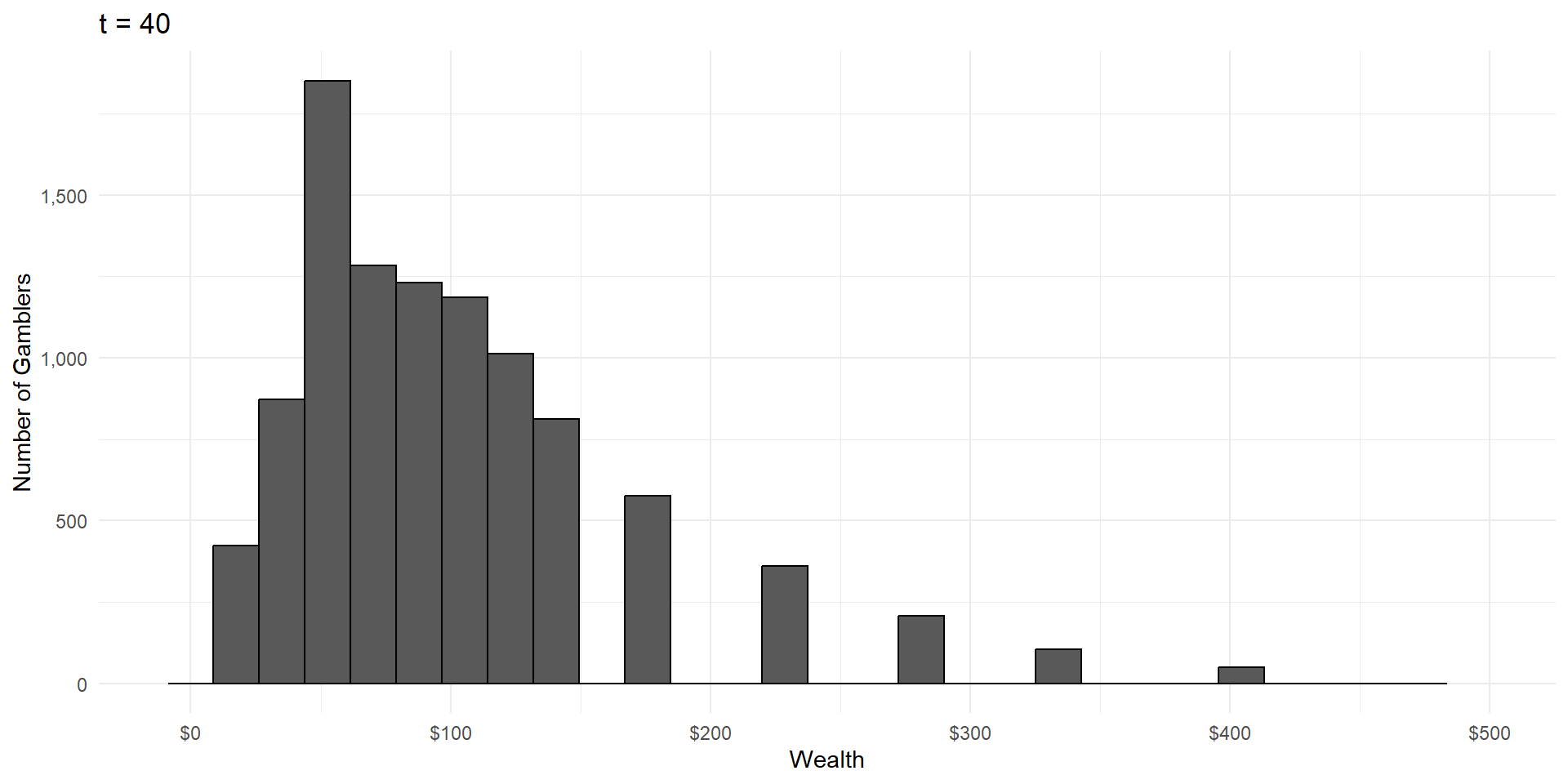
Violation 1: Multiplicative Processes
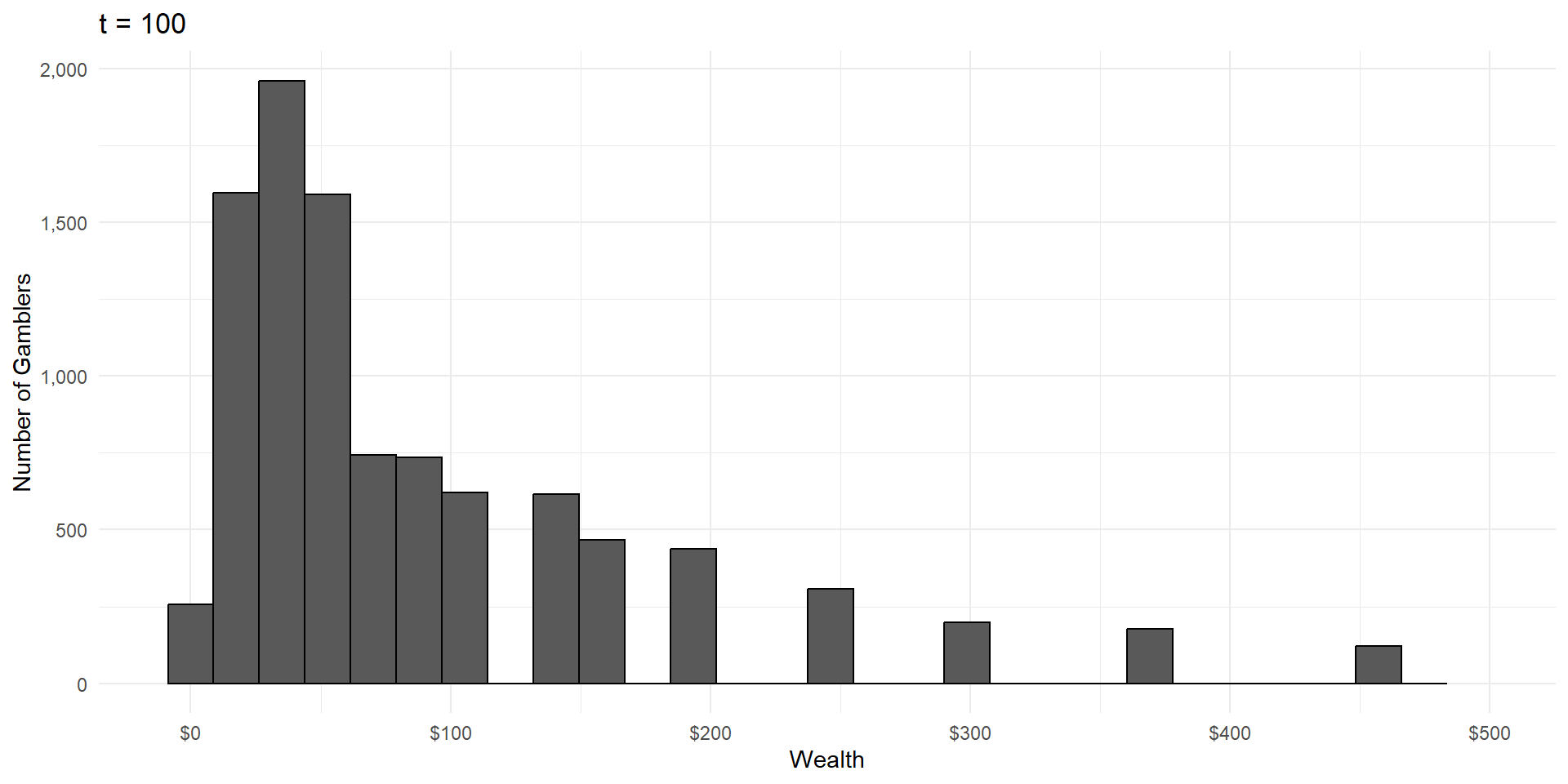
Violation 1: Multiplicative Processes
Violation 1: Multiplicative Processes
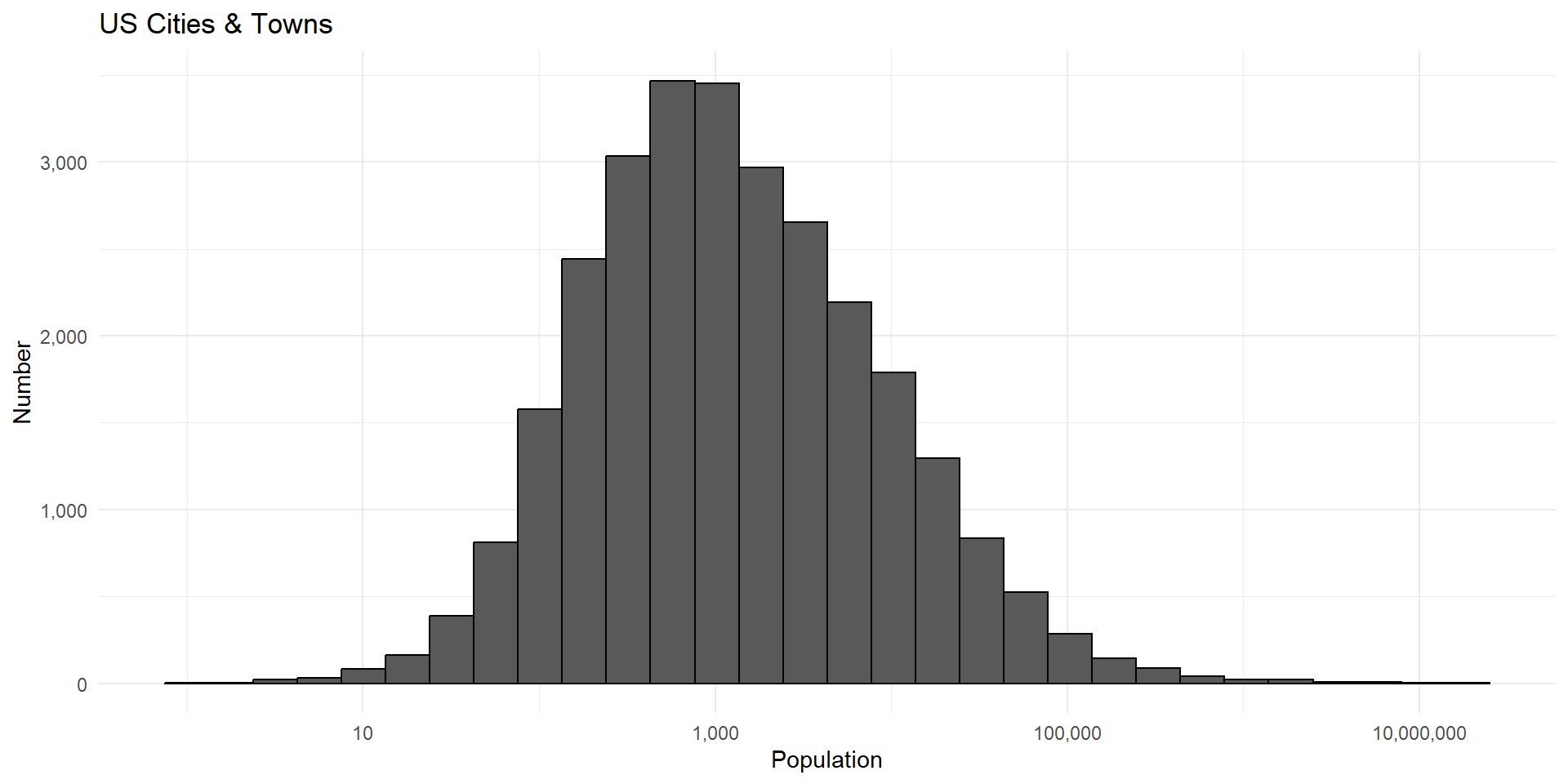
This is called a lognormal distribution, because here’s what it looks like on a logarithmic scale:
Lognormal Distributions
Lognormal distributions are common when outcomes are the result of multiplicative growth over time.
For example, the distribution of city sizes in the United States.
Lognormal Distributions
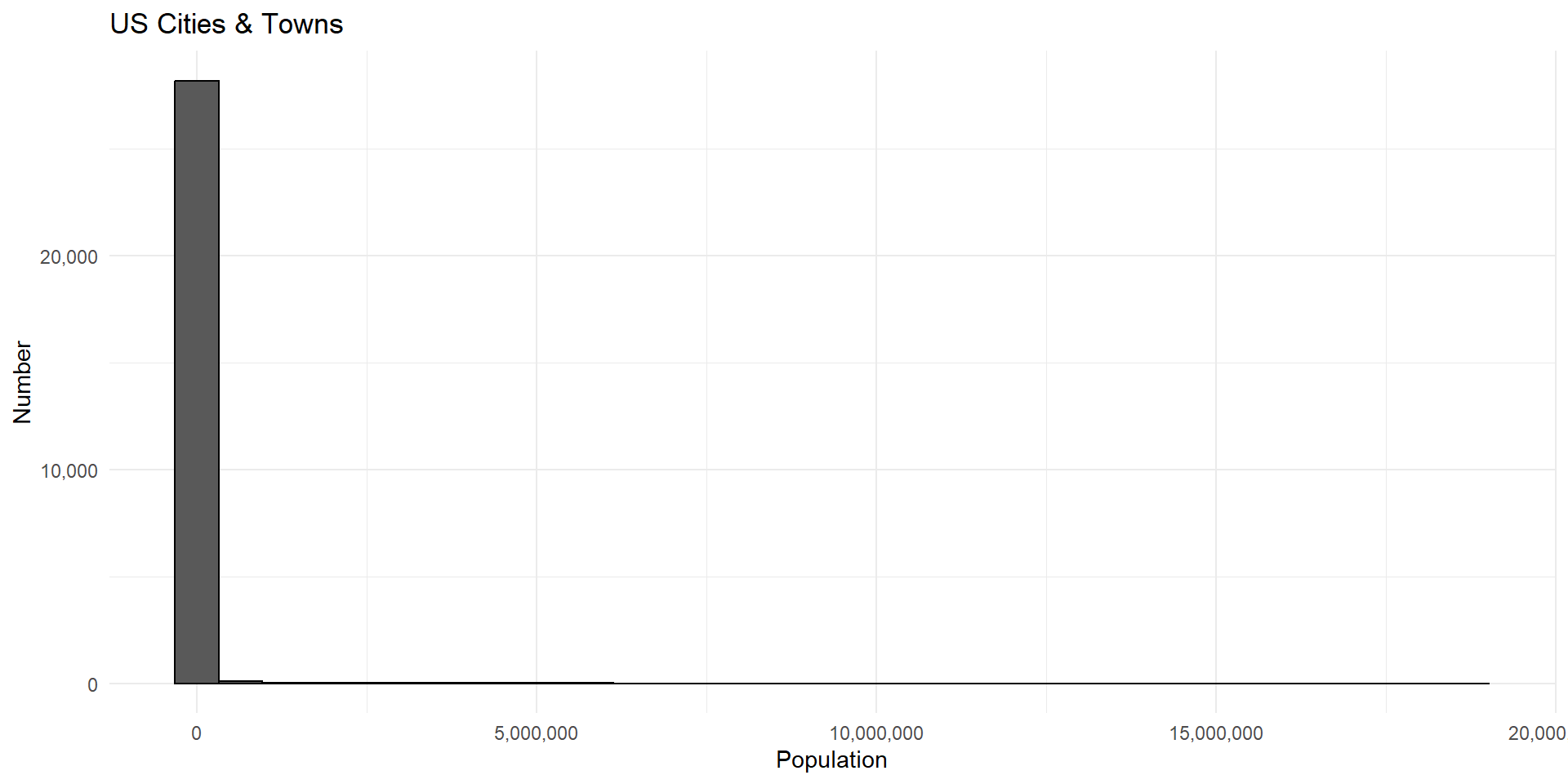
Lognormal Distributions
Violation 2: Interdependence
Next, let’s consider what happens when the independence assumption of CLT is violated.
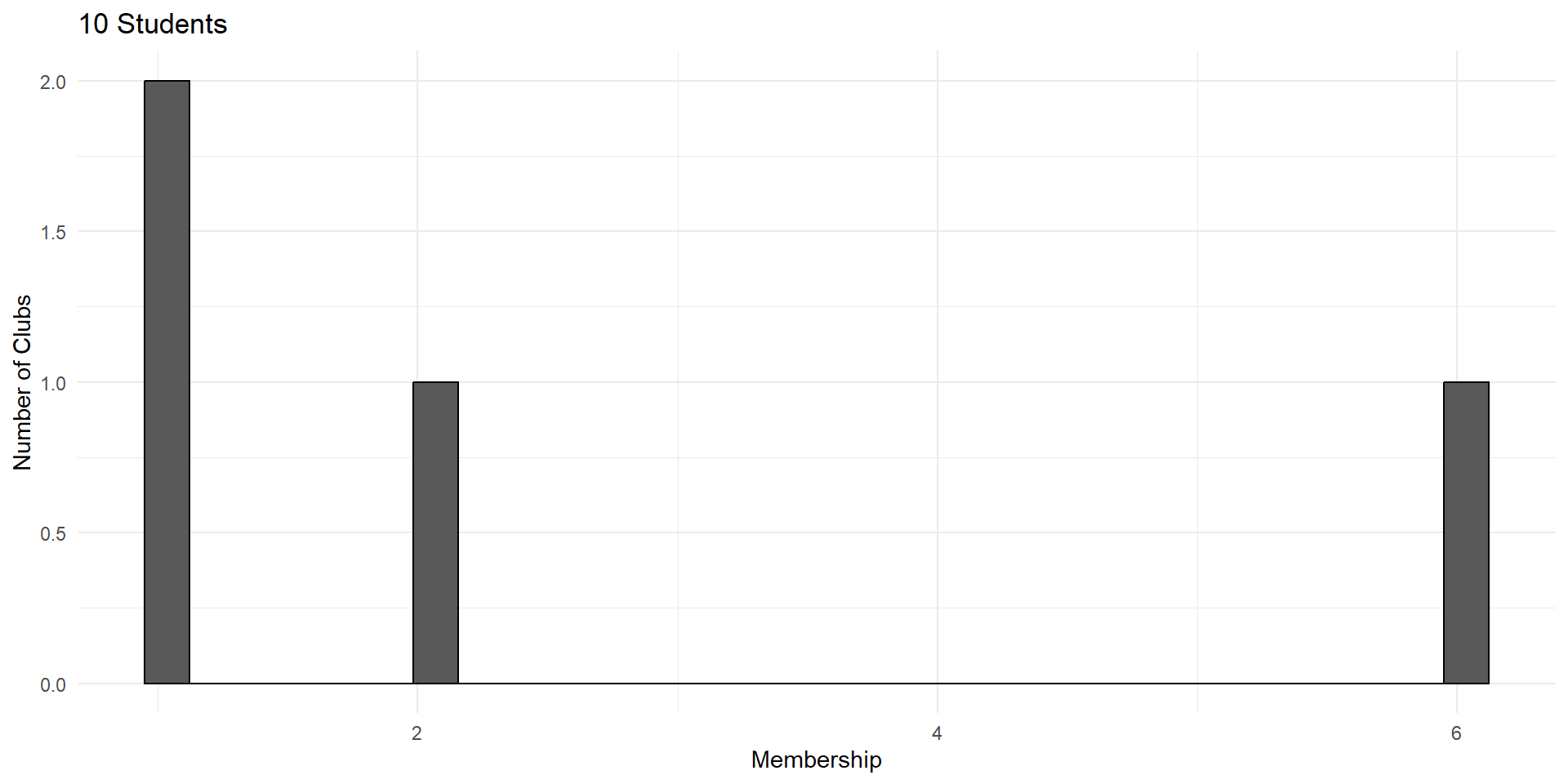
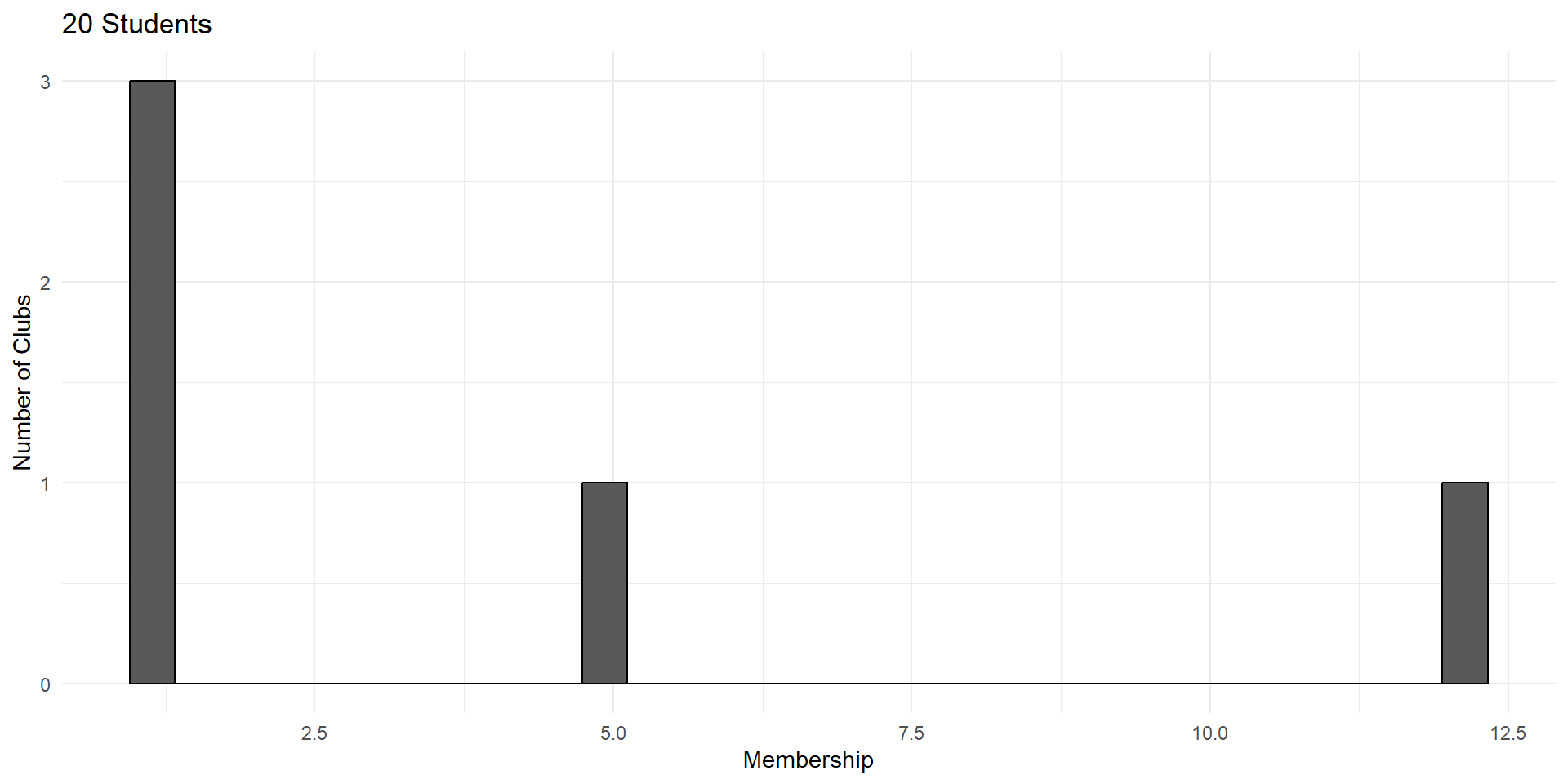
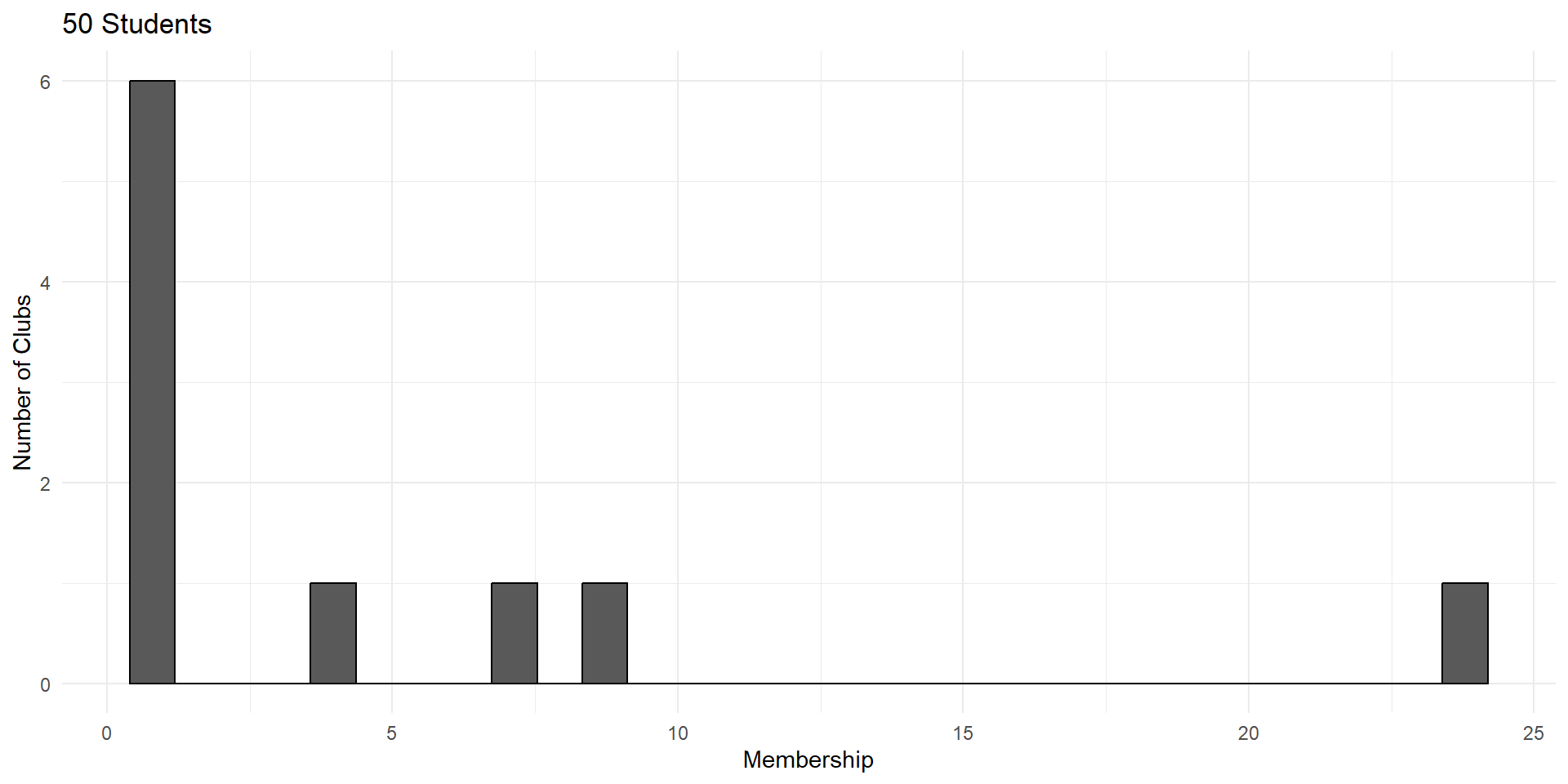
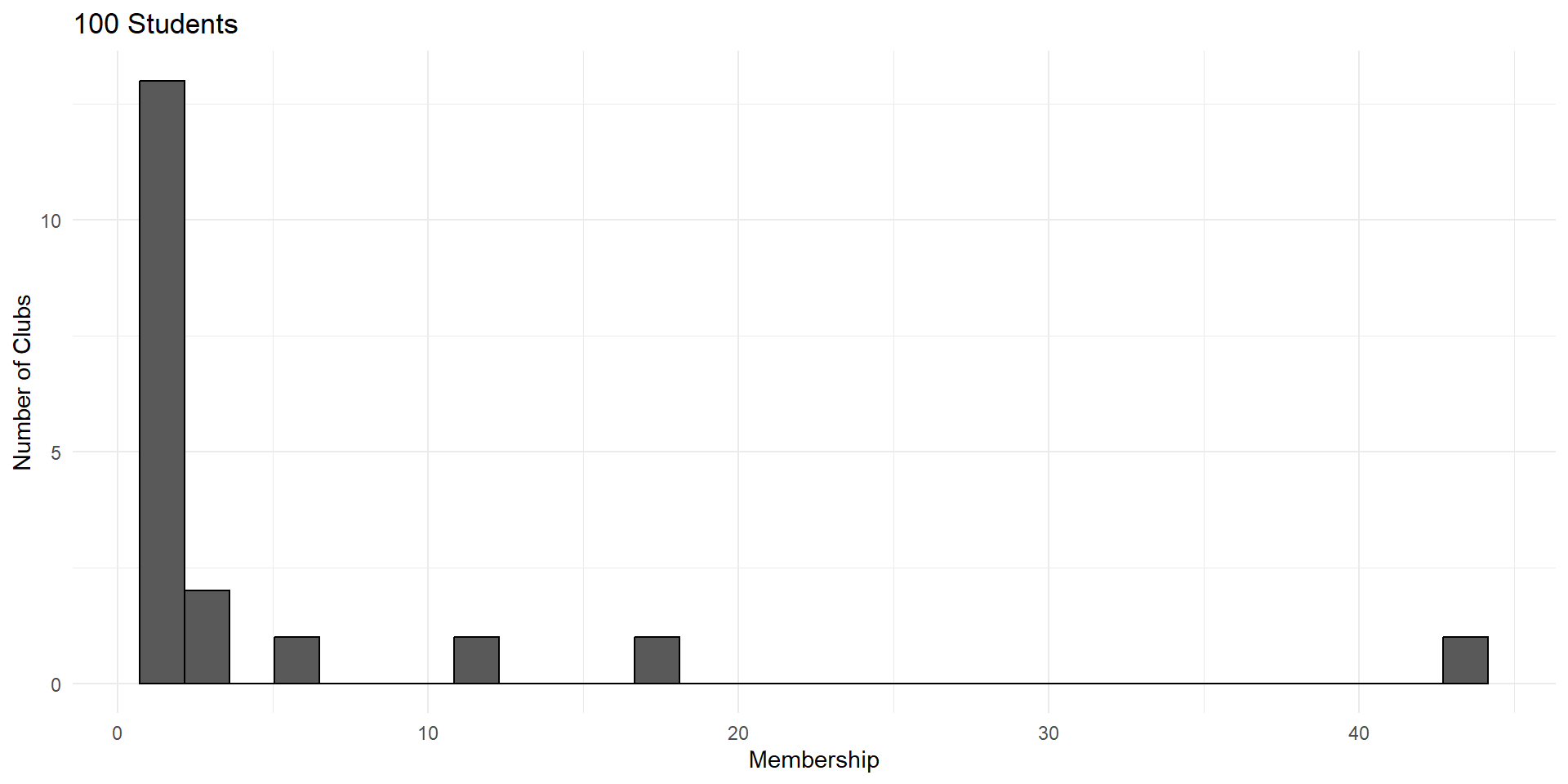
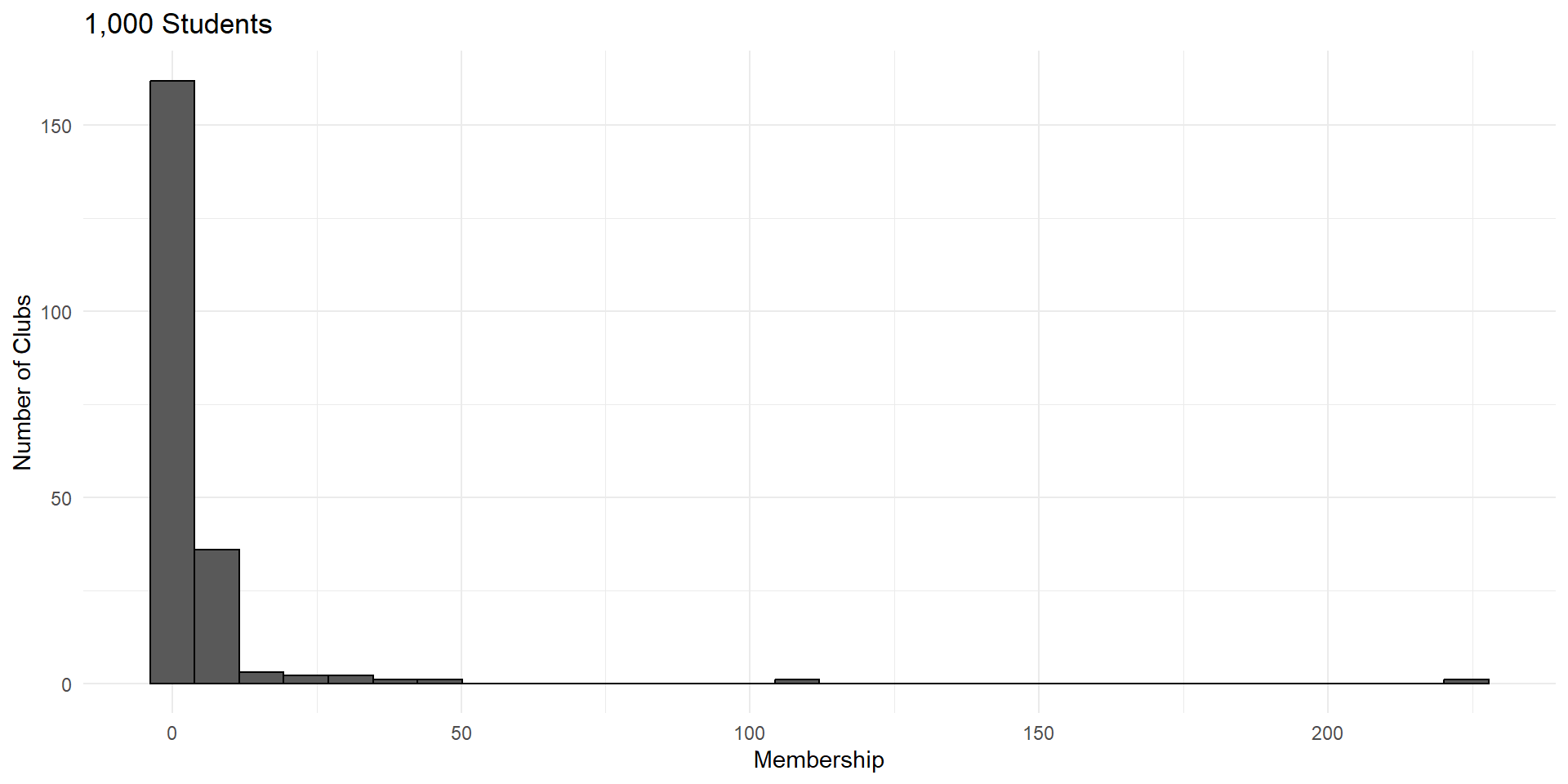
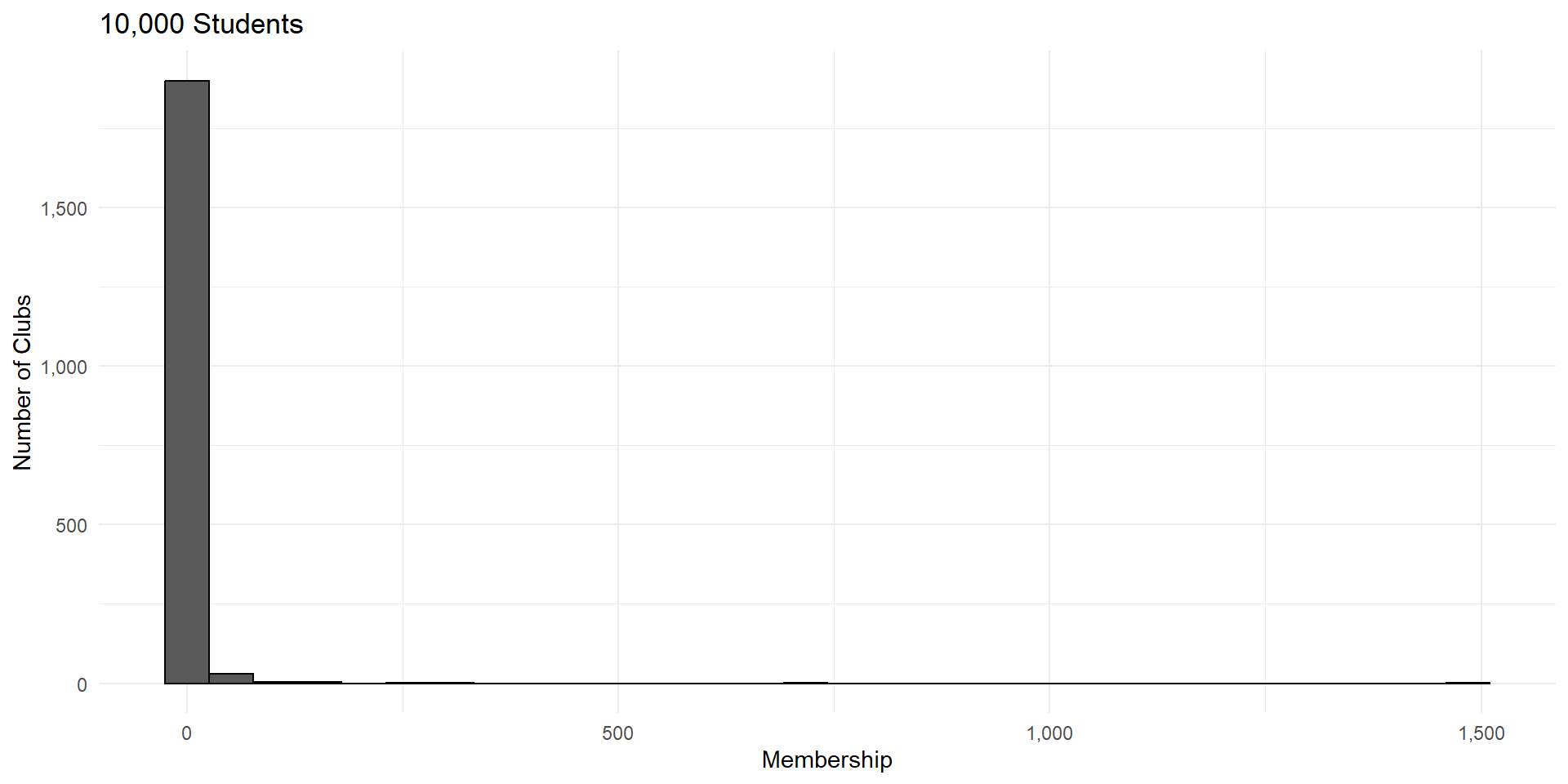
Imagine a process of students forming clubs.
Each student can choose either to start a new club or join an existing club.
This process exhibits “preferential attachment”. You’re more likely to join a popular club.
So club size is the sum of a large number of student choices.
But these choices are not independent. A club is more likely to grow if it’s already popular.
Violation 2: Interdependence
Violation 2: Interdependence
Violation 2: Interdependence
Violation 2: Interdependence
Violation 2: Interdependence
Violation 2: Interdependence
Power Laws
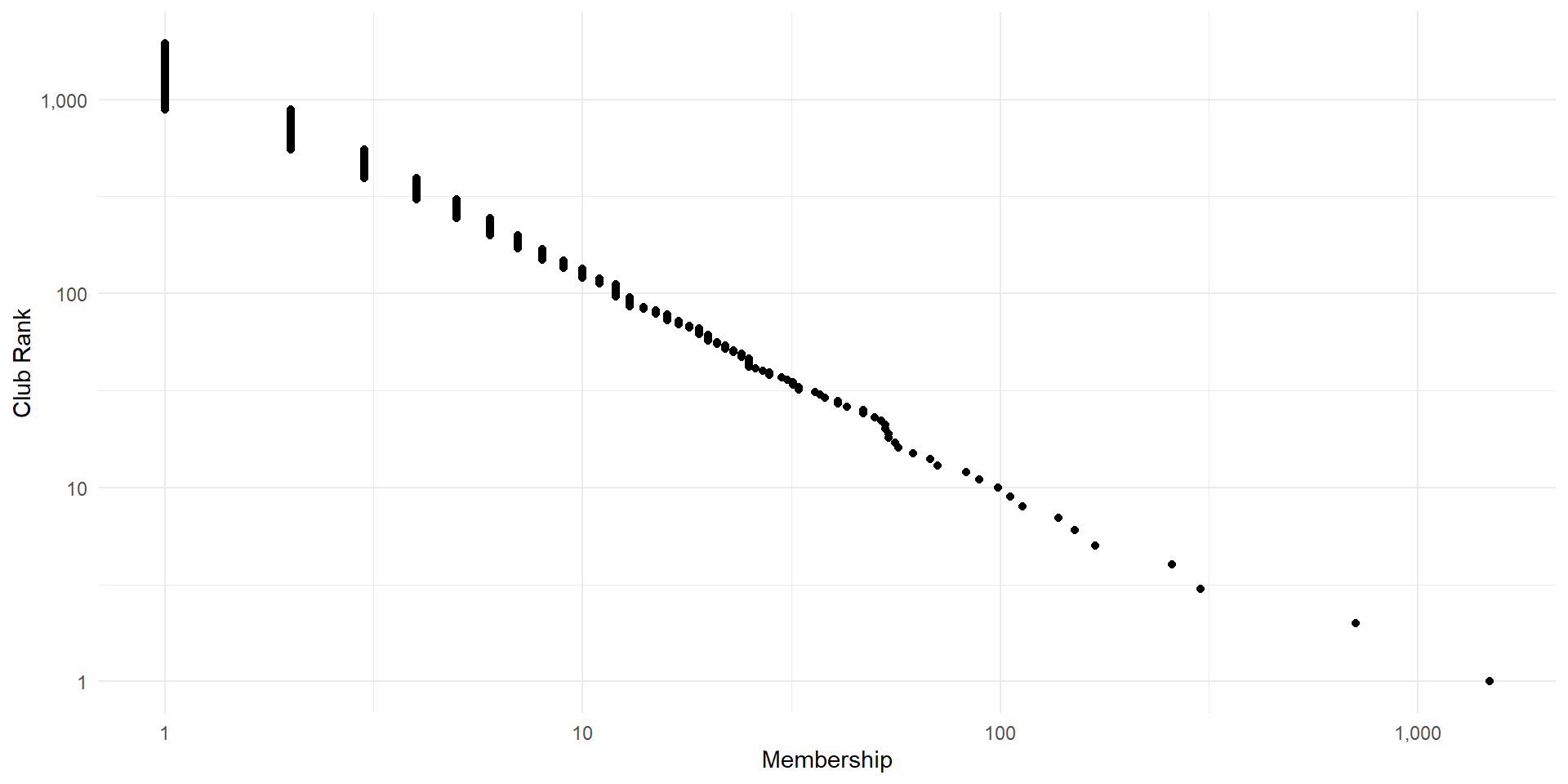
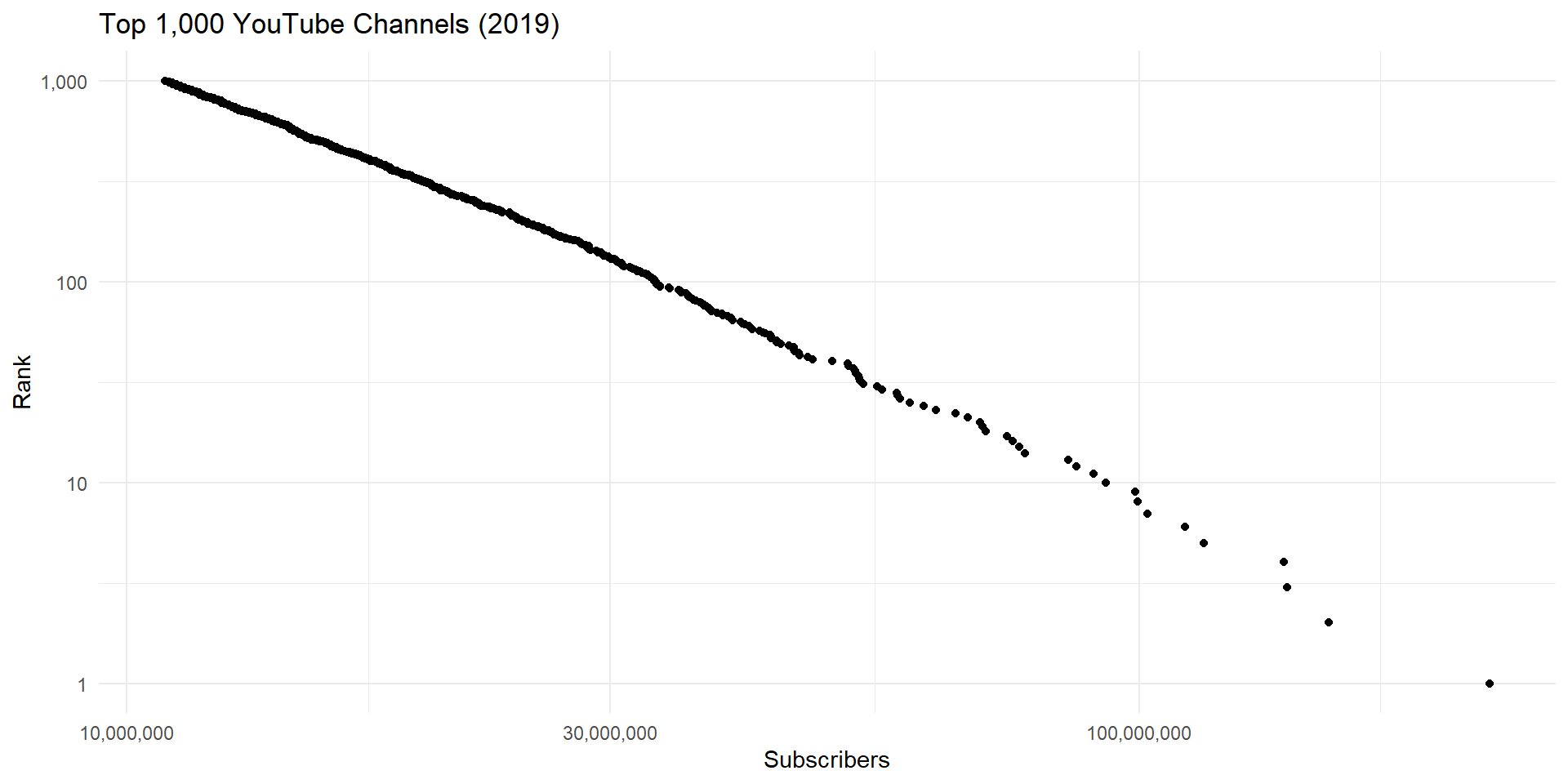
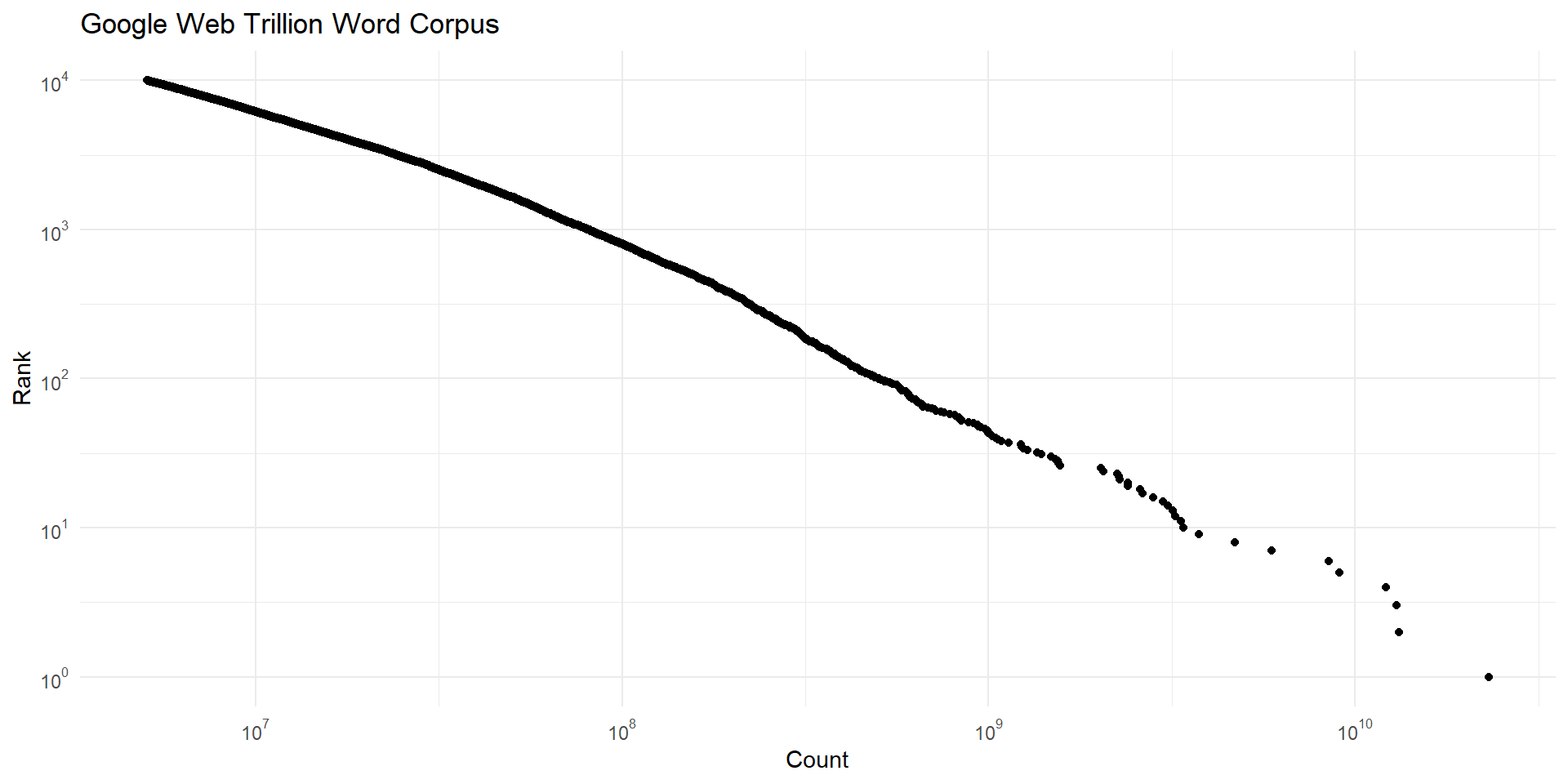
Distributions generated by this type of process are called power laws. They have a very distinct shape.
Power Laws
Power Laws
Power Laws
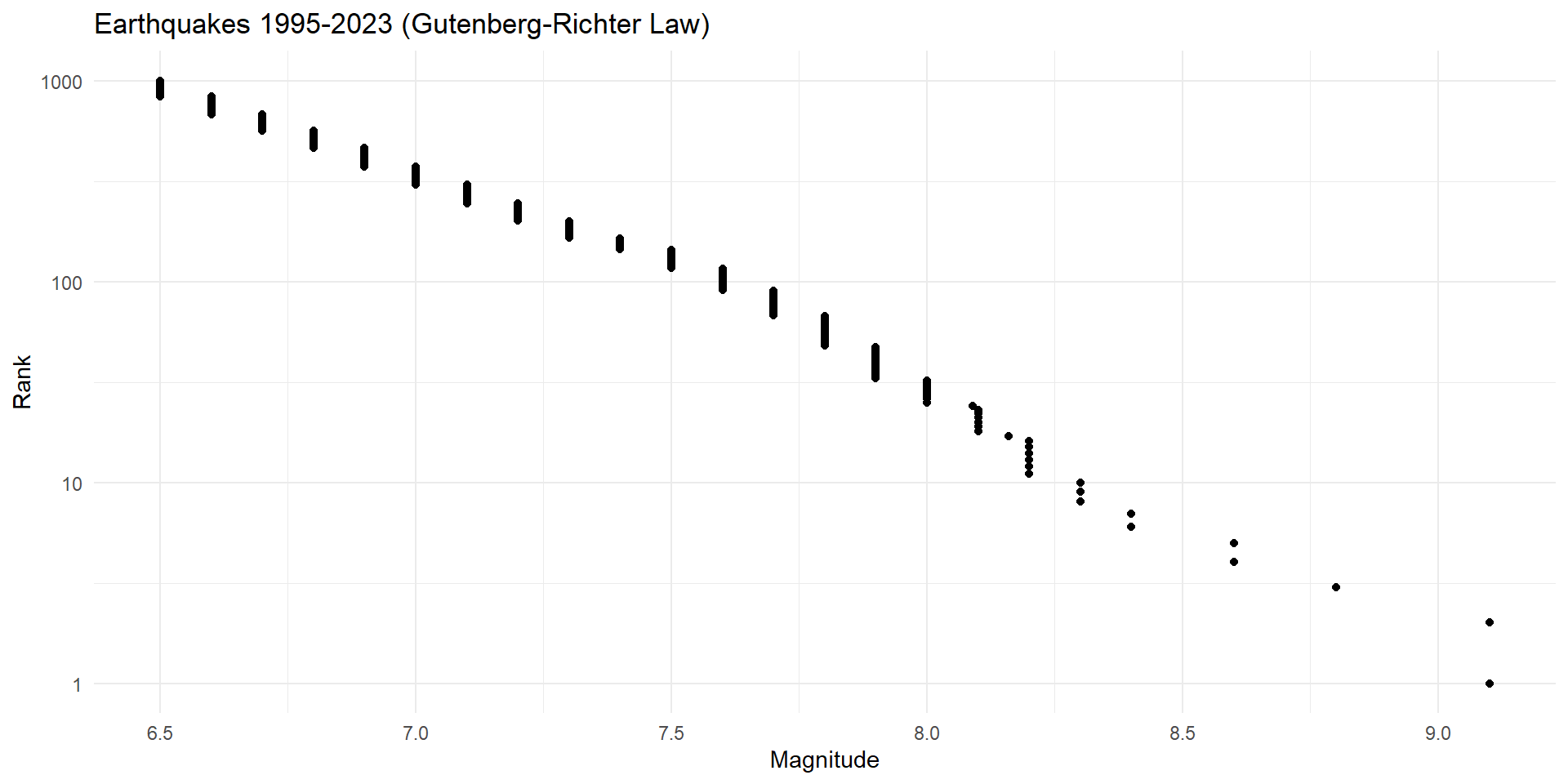
Power Laws
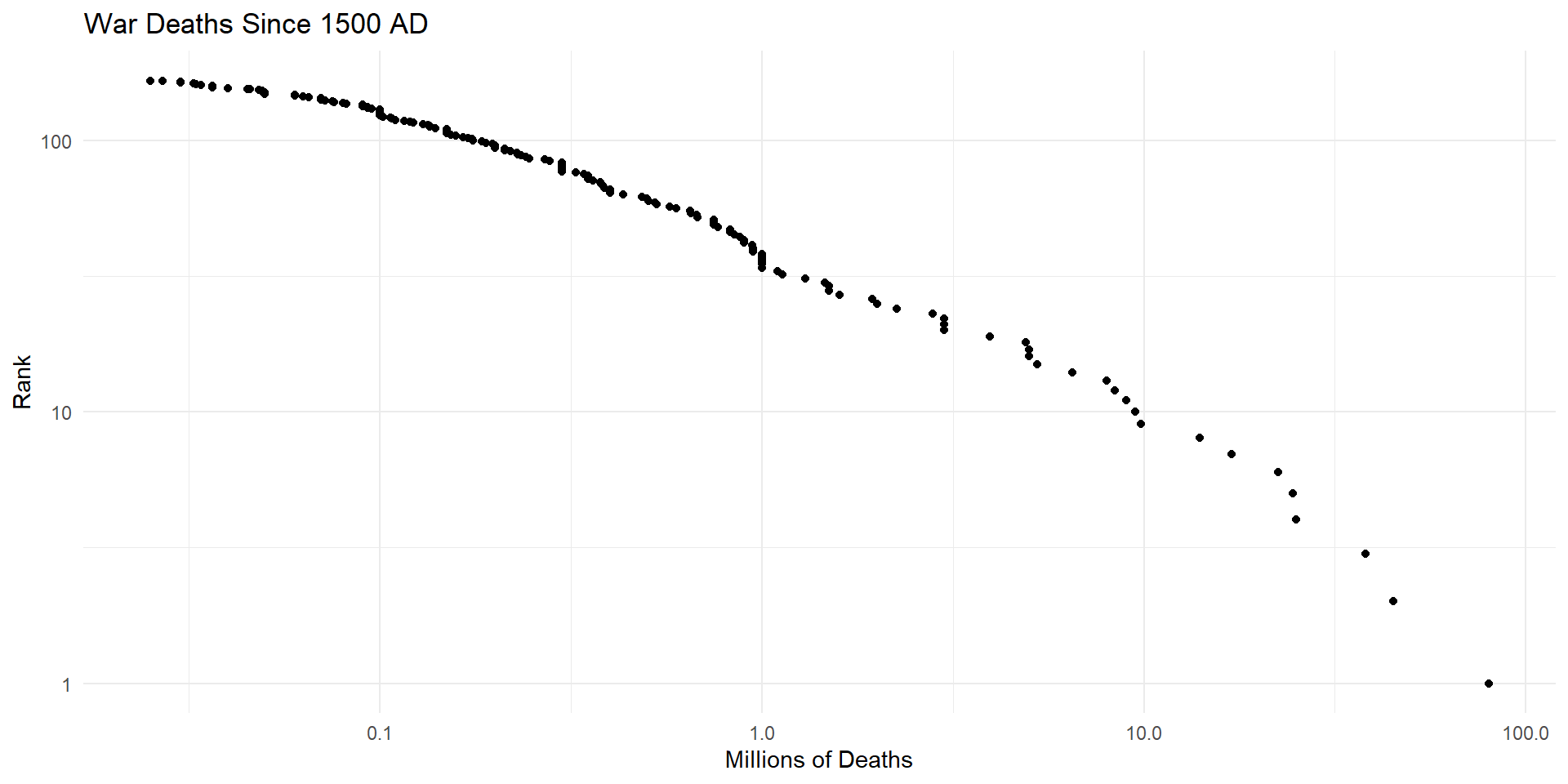
Power Laws
Power laws are the result of processes where large events are more likely grow than small ones.
Each of these outcomes – social media subscribers, word usage, earthquakes, armed conflict – exhibit “snowball effects”.
This violates the independence assumption of CLT.
Takeaways
If your outcome falls on a bell curve, then tail risk is low. Remember 68-95-99.7%.
But if the sum or independence assumptions of CLT are violated, expect to observe much longer tails.
Lognormal and power law distributions are dominated by extreme events, when occur much more frequently than the bell curve would suggest.