Path Dependence
POLS 3220: How to Predict the Future
Warmup
Consider the following scenario:
Two basically-identical products hit the market.
At first, two people own Yeti and one person owns a Stanley.
New costumers are more likely to buy popular cups (positive feedback).
Assume that every time a new person wants to buy a cup, they choose a person at random and buy whatever cup they own.
If we let this process play out, what percent of people do you think will own a Yeti in equilibrium?

Warmup
Good news: everyone is right!
In a process like the one we just described (pick a random person and copy them) literally anything can happen.
But the final outcome depends very strongly on what happens with the first few buyers.
Warmup

Path Dependence
This illustrates the concept of path dependence.
- Many different outcomes are possible in equilibrium, and which one we observe depends on the exact sequence of historical events (i.e. which “path” was taken).
Path Dependence
Metaphor: Cow Paths
Why is there a path there?
- Because that’s where the cows walk.
Why do the cows walk there?
- Because that’s where the path is!
There’s no “deep” reason why the cow path formed in that particular spot.
Just a somewhat random set of choices the cows made early on that got reinforced over time.

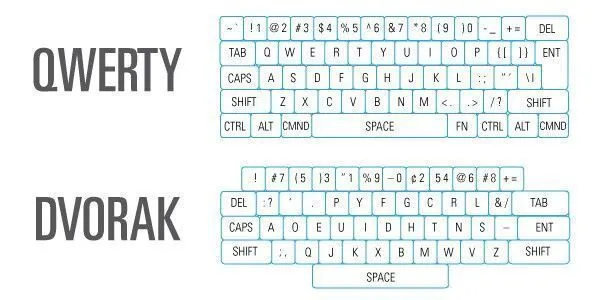
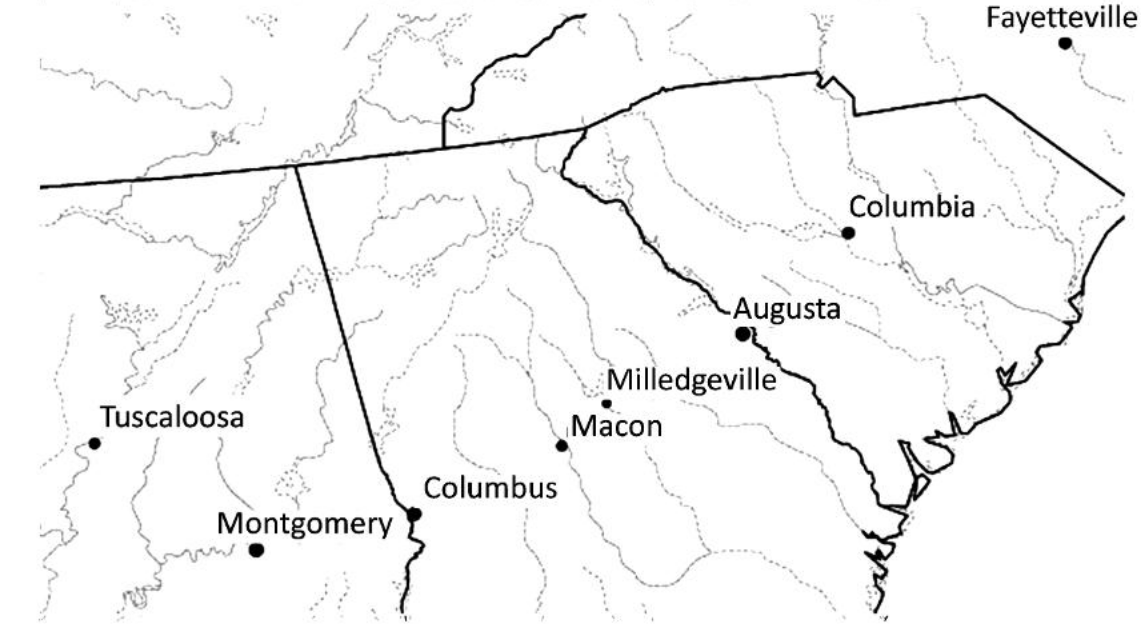
Examples of path dependence
Examples of path dependence
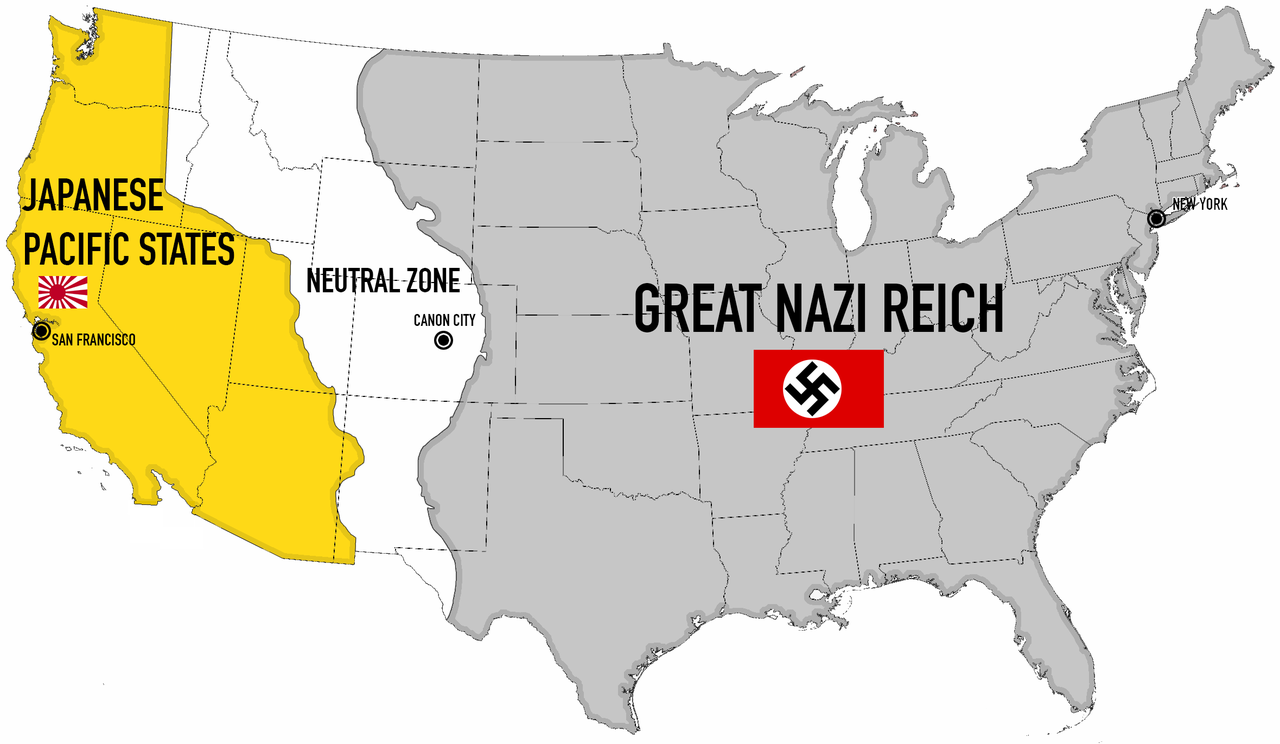
What If?
If outcomes are path dependent, then some points in time have a disproportionate impact on how history will unfold.
Social scientists call these points critical junctures.
Critical junctures are a staple of the alternative history genre: identifying key points in time where, if one small thing changed, it would create an entirely new timeline.

Path Dependence and Prediction
Path dependence makes long-term forecasting basically hopeless.
So when should we expect that outcomes will be path dependent?
Back to our old friend, the ergodic theorem.
As we showed previously, an ergodic process always has a unique equilibrium outcome.
It follows that these sorts of processes can’t be path dependent.
No matter what happens, the system moves inexorably towards that equilibrium.
Ergodic Systems Aren’t Path Dependent
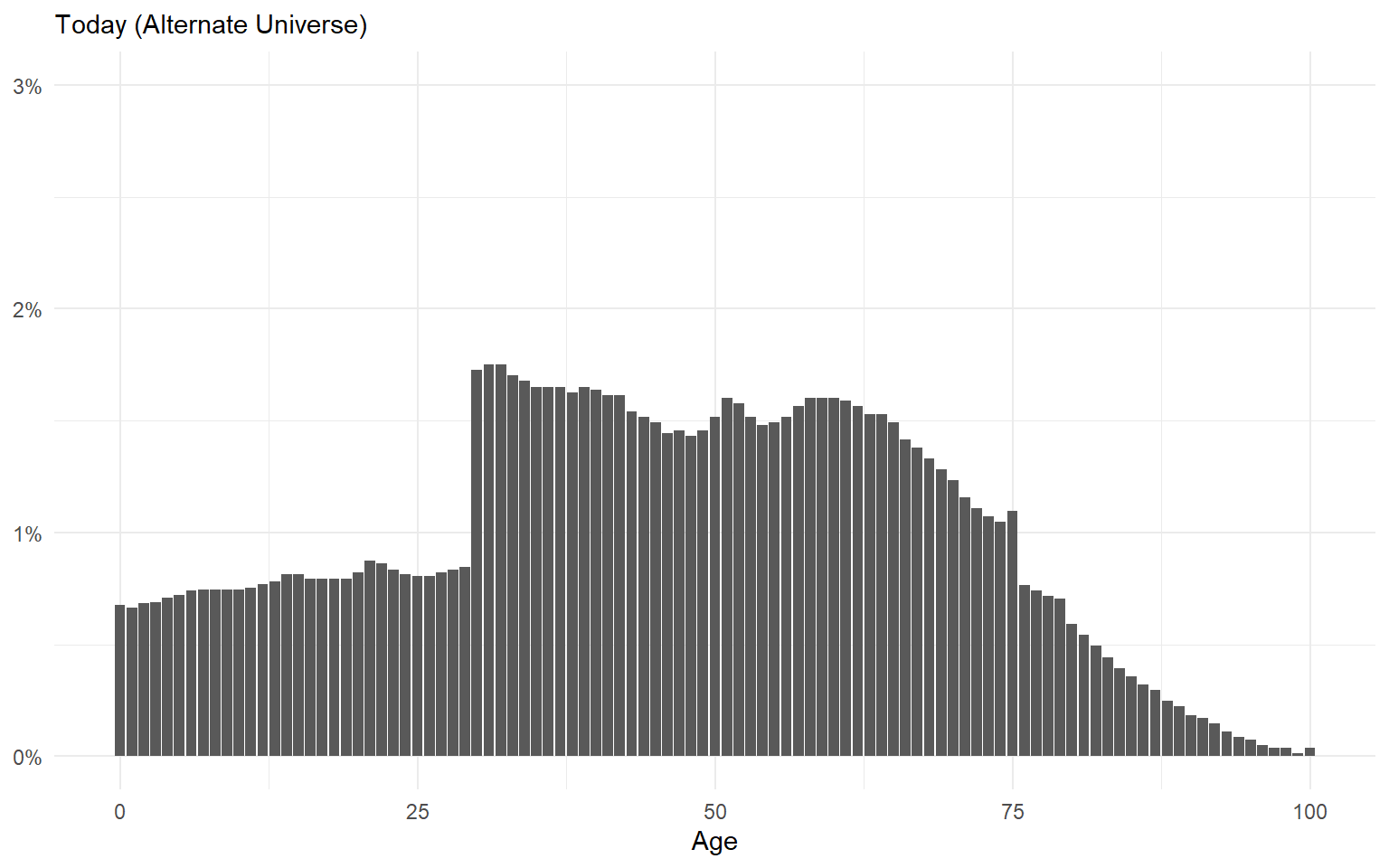
Ergodic Systems Aren’t Path Dependent
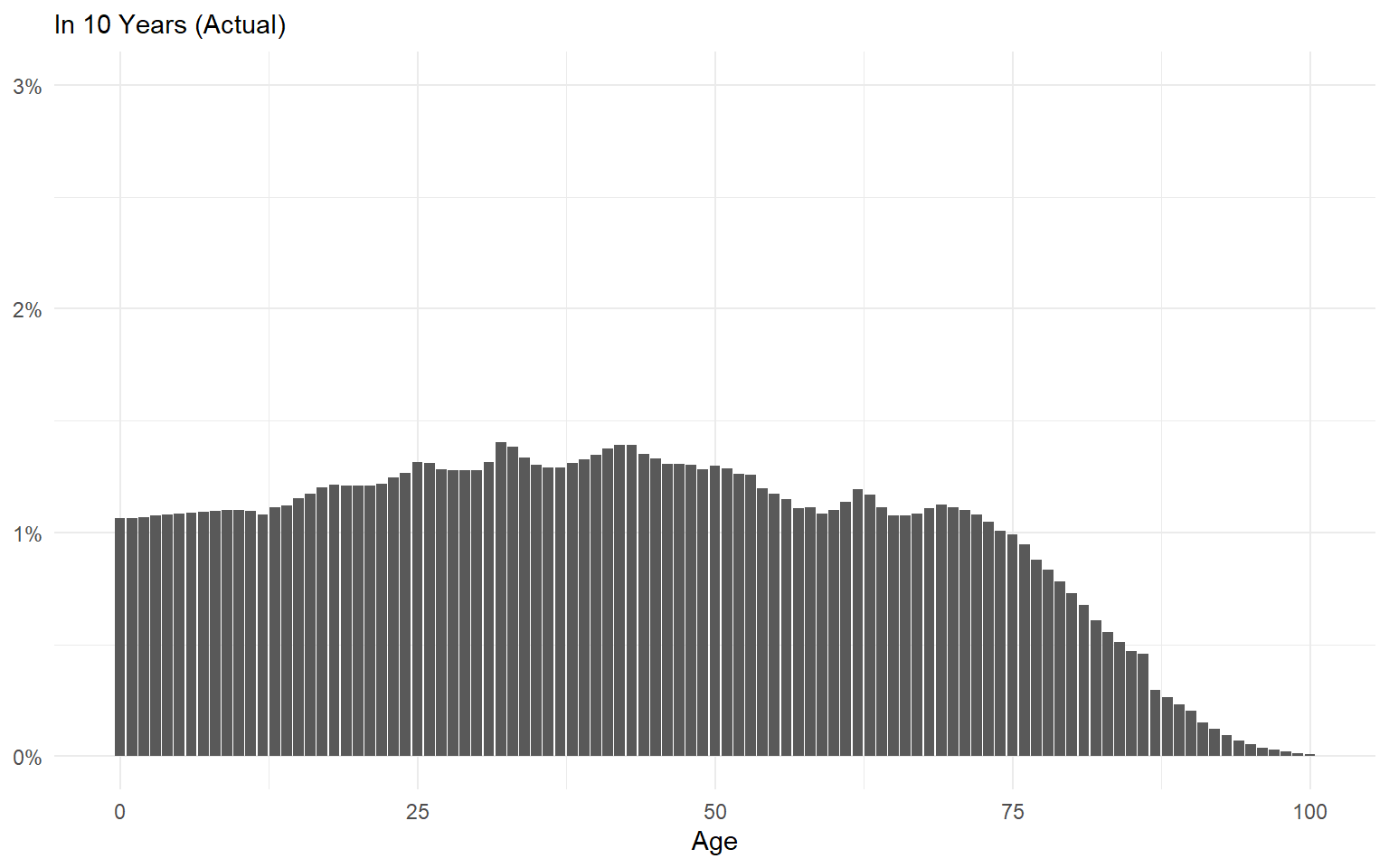
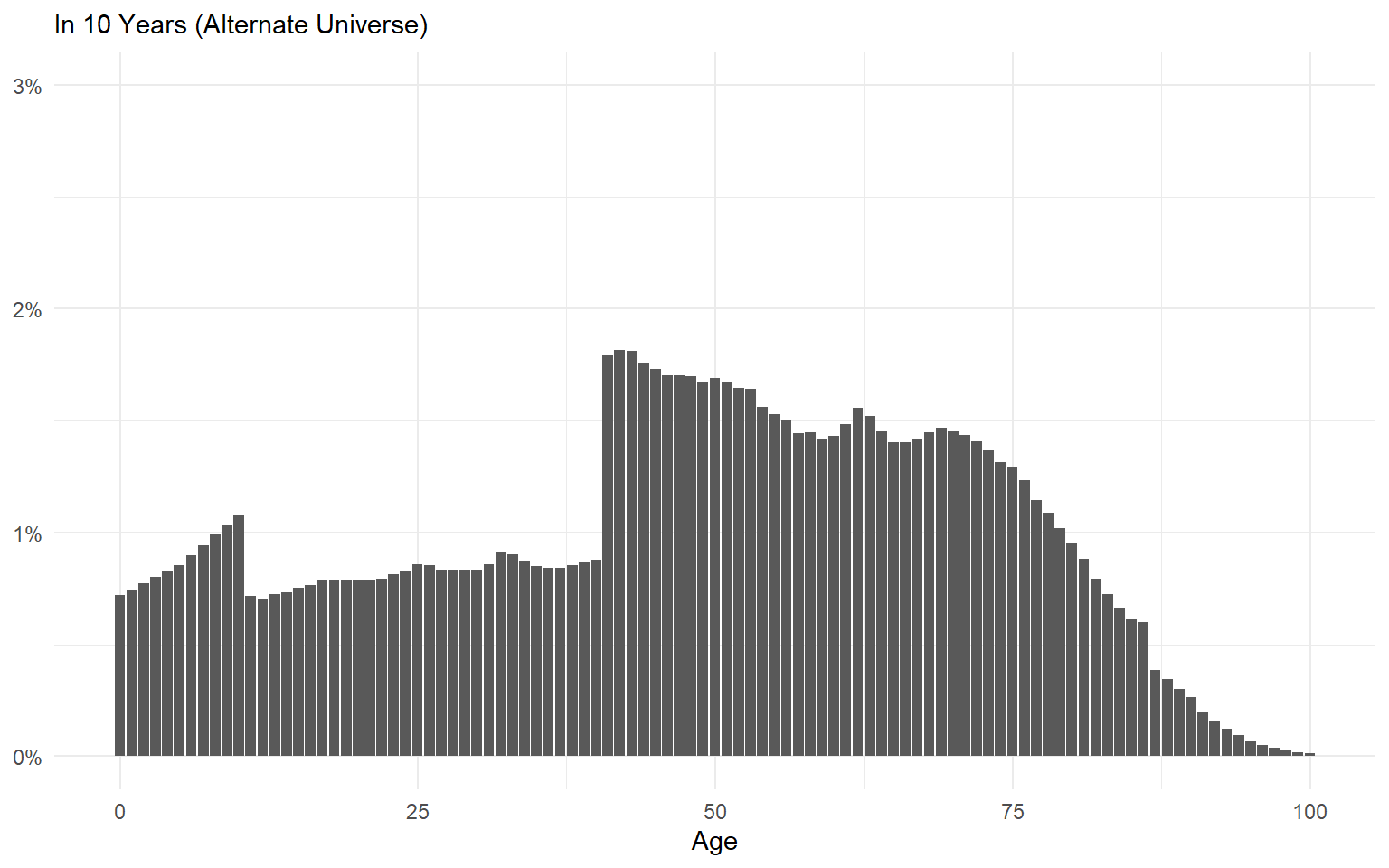
Ergodic Systems Aren’t Path Dependent
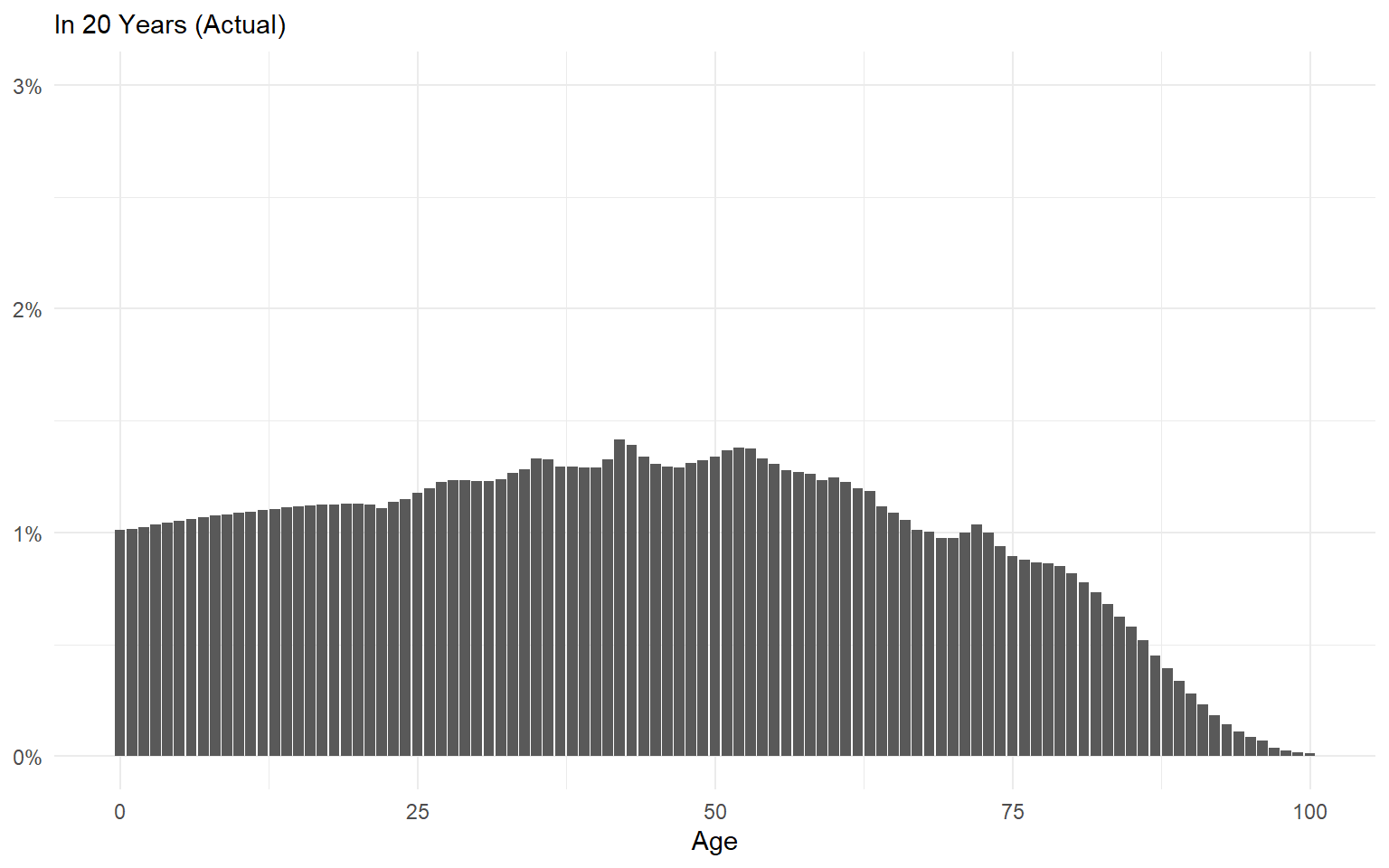
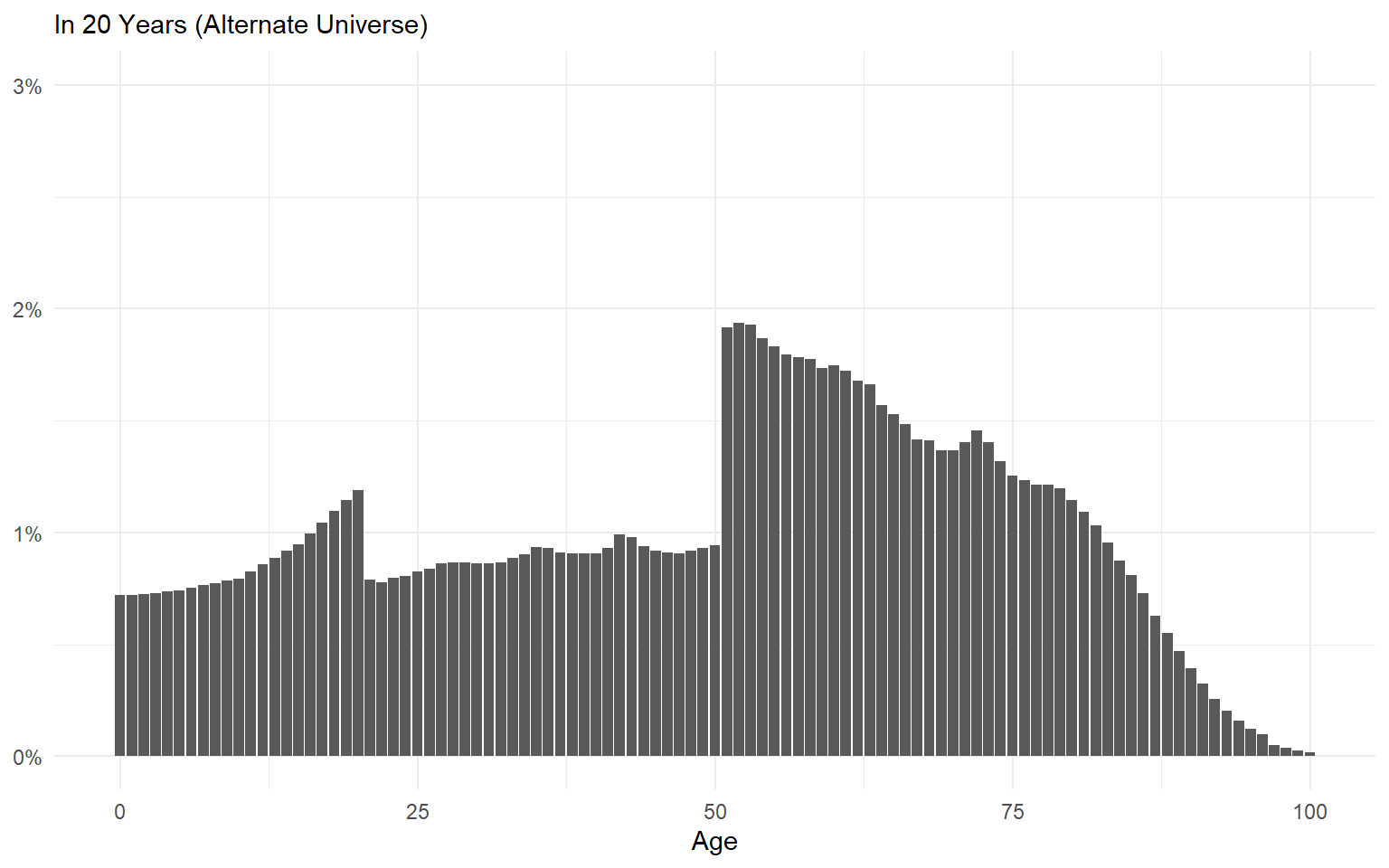
Ergodic Systems Aren’t Path Dependent
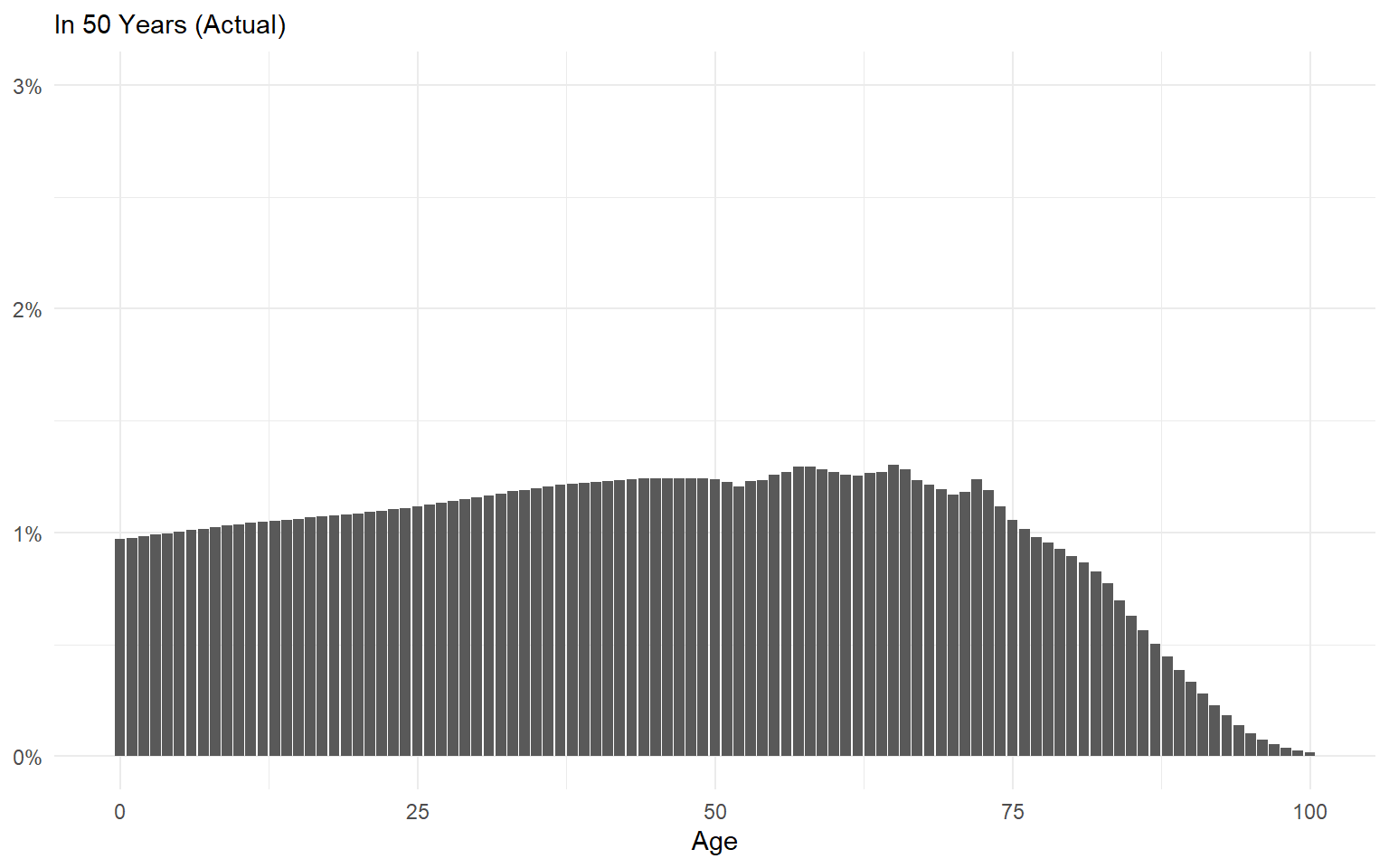
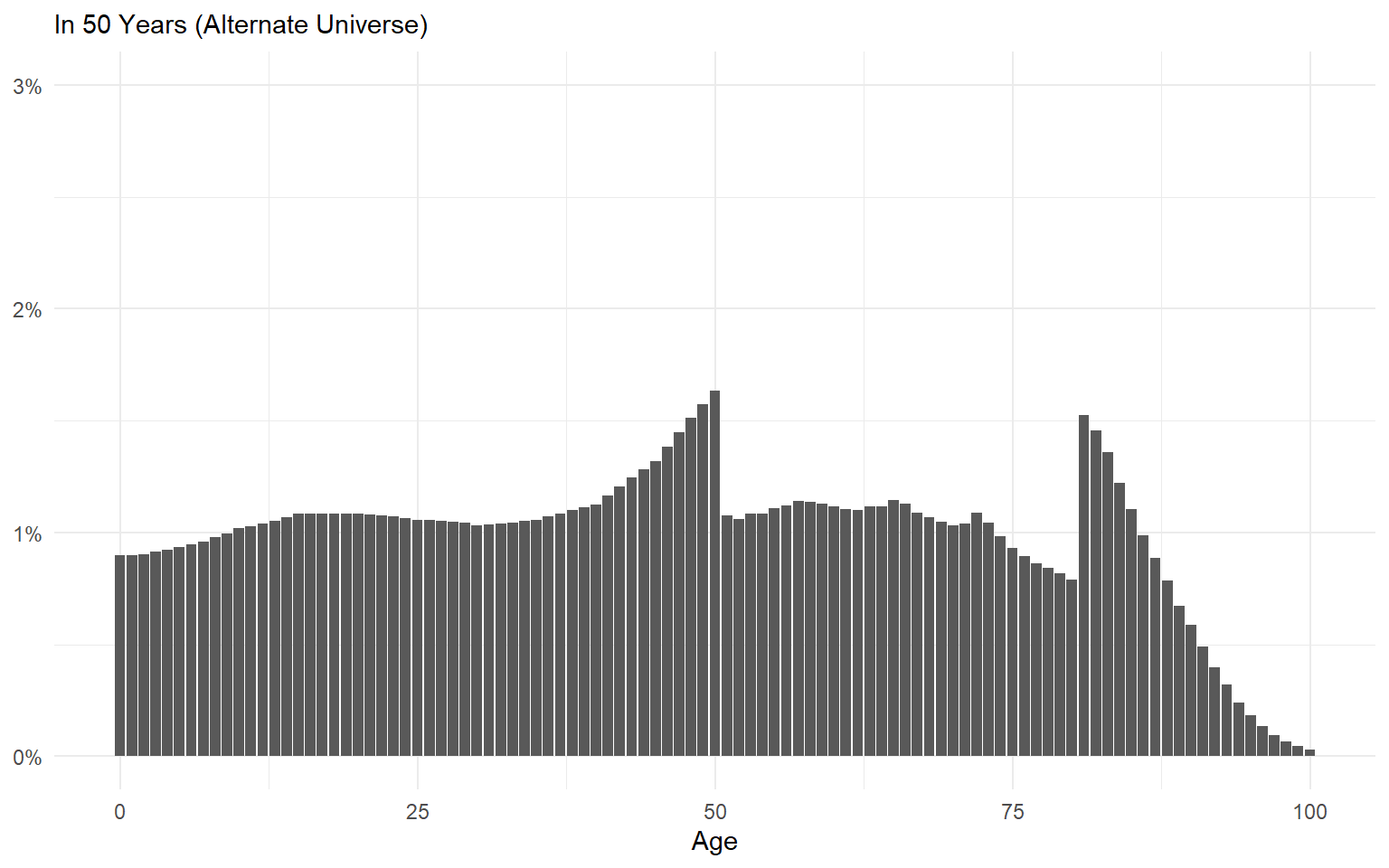
Ergodic Systems Aren’t Path Dependent
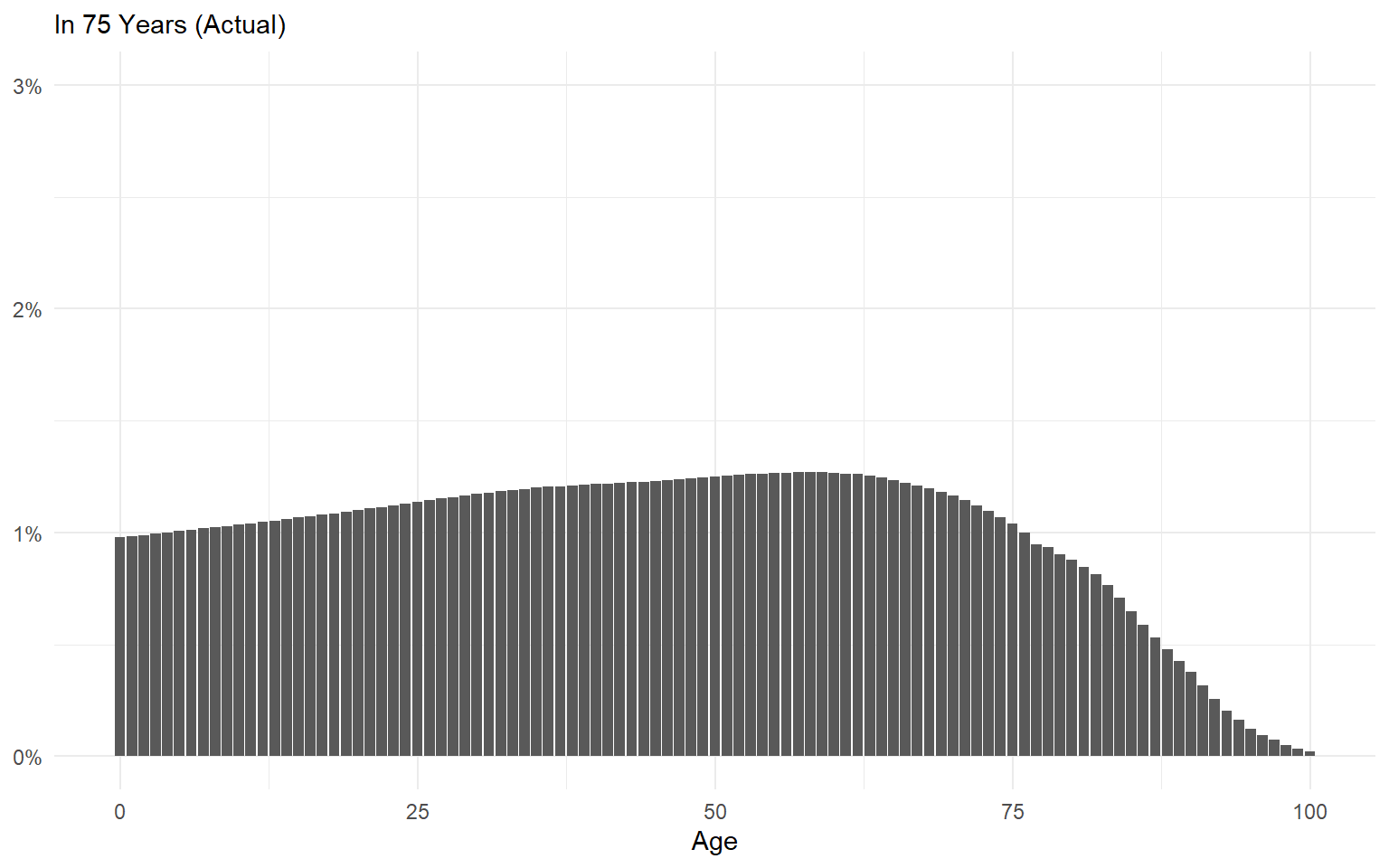
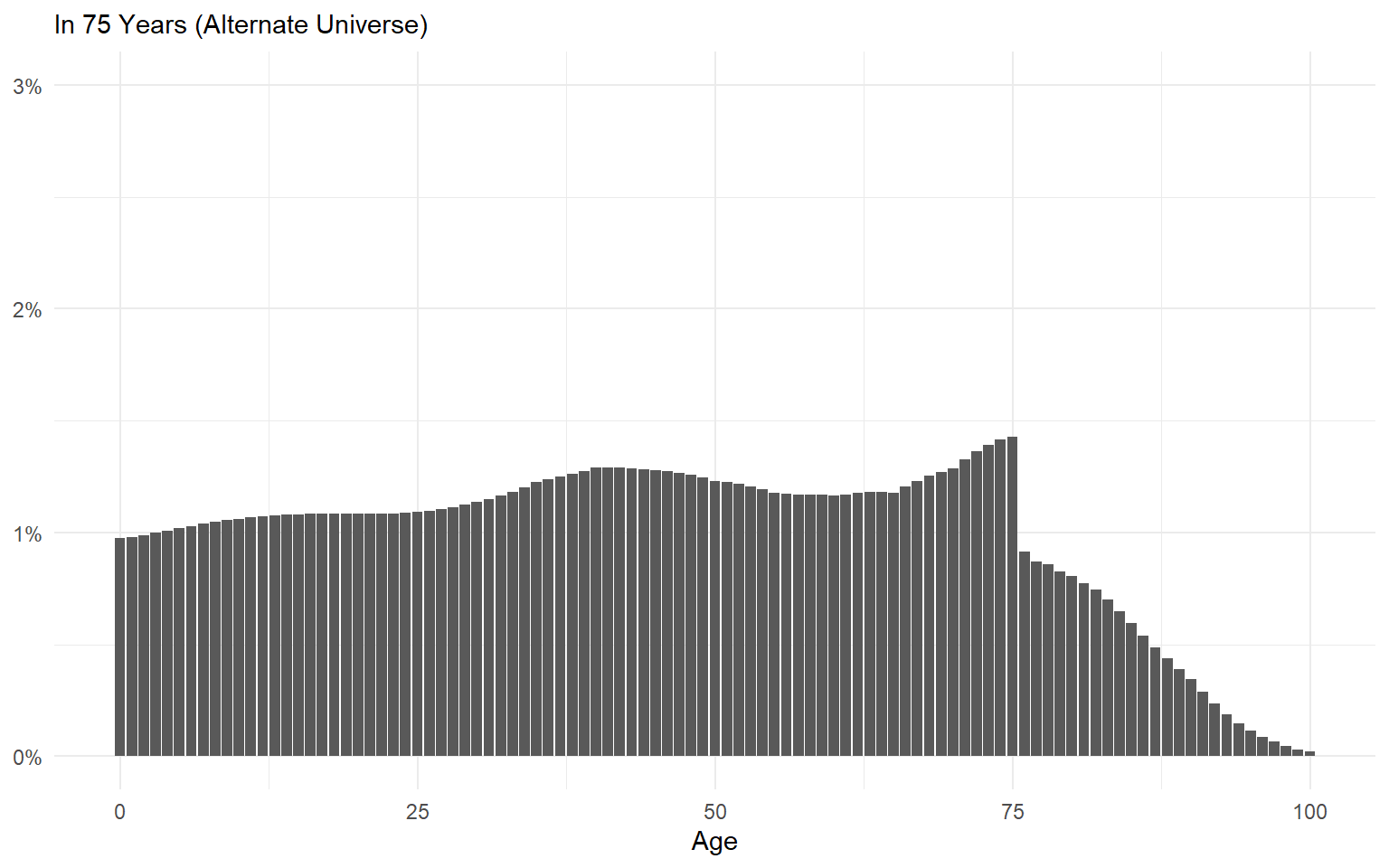
Ergodic Systems Aren’t Path Dependent
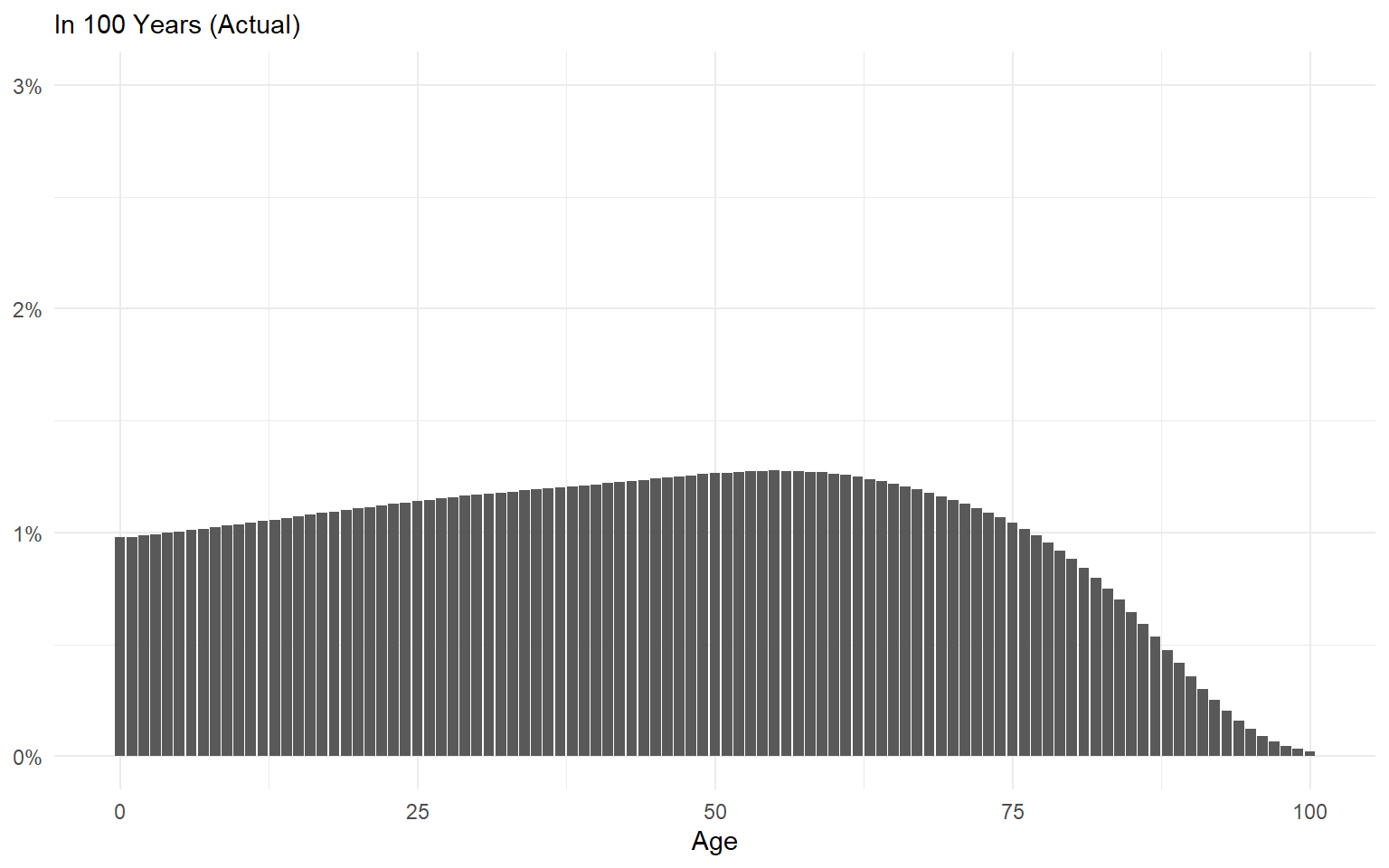
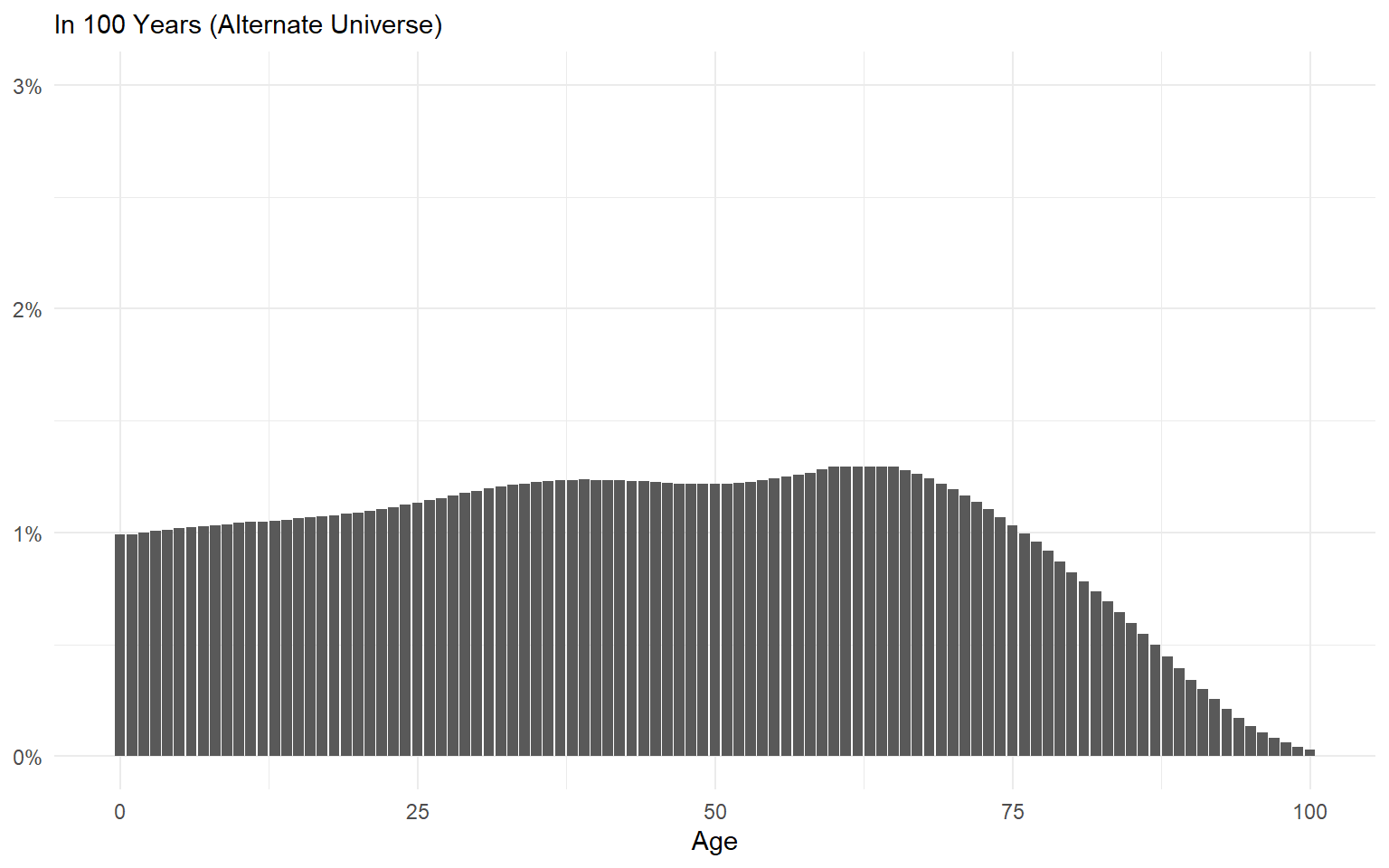
Conclusion
Path dependence should make us humble about our ability to make long-term predictions.
Correctly identifying critical junctures ahead of time is practically impossible.
We can be a bit more confident if the system in question is ergodic.