Tree Models

POLS 3220: How to Predict the Future

Today’s Agenda

• Last time, we introduced linear models as a machine learning tool.

  • The key idea was to make predictions based on a linear combination of predictor variables.

• Today, we’ll discuss an approach that combines variables in a nonlinear fashion, called classification and regression trees (CART).

  • It looks exactly like the probability trees we worked with in the first half of the semester.

  • Except we let computer to build them for us!

Motivating Problem

• Can we predict a movie’s Rotten Tomatoes rating?

• Predictor Variables: Content Rating, Genre, Release Date, Distributor, Runtime, Number of Audience Reviews

Outside View

If we had no other information, what would we predict based solely on historical base rates?

. . .

Rating	Total	%
	3,259	18.4
	6,844	38.7
	7,565	42.8

. . .

We can do better!

Classification Trees

• A classification tree works by recursively partitioning the dataset (i.e. repeatedly splitting the data into smaller subsets).

. . .

Classification Trees

With each partition, your prediction becomes less biased.

. . .

Criterion, Searchlight, or A24

Rating	Total	%
	118	37.2
	135	42.6
	64	20.2

Other Distributors

Rating	Total	%
	3,105	18.4
	6,396	37.9
	7,357	43.6

Classification Trees

With each partition, your prediction becomes less biased.

. . .

Audience Count < 10,000

Rating	Total	%
	1,293	12.0
	5,052	46.9
	4,427	41.1

Audience Count >= 10,000

Rating	Total	%
	1,811	30.8
	1,193	20.3
	2,870	48.9

Choosing Splits

• What is the “best” way to partition the data?

• Up to now, we’ve been choosing our splits based purely on vibes.

• A more principled way is to partition the data based on how much information it reveals.

Information Theory: Review

Recall the definitions of information and entropy.

• Information is how surprised we are when we learn an outcome. Equal to \(-log(p)\).

• Entropy is “expected surprise”: how much surprise we experience on average when we learn the outcome.

• If we could perfectly predict the Rotten Tomatoes rating a of movie, then entropy would be zero. (We would never be surprised).

• Therefore, our optimal strategy is to seek out information that reduces entropy as much as possible.

Information Theory: Review

Rating	Total	p
	3,259	0.184
	6,844	0.387
	7,565	0.428

Information Theory: Review

Rating	Total	p	-log(p)
	3,259	0.184	2.44
	6,844	0.387	1.37
	7,565	0.428	1.22

. . .

\(\text{Entropy} = -\sum p\times log(p)=\) 1.5 bits.

Information Gain

• Each time you partition the dataset, it reduces entropy.

• This is because you become more certain about your prediction, therefore less likely to be surprised!

• The information gain from a partition equals how much it reduces entropy.

Information Gain

Audience Count < 9,000

Rating	Total	%
	1,328	12.1
	5,161	47.1
	4,462	40.7

Entropy: 1.41 bits

Audience Count >= 9,000

Rating	Total	%
	1,894	31.5
	1,219	20.3
	2,899	48.2

Entropy: 1.5 bits

Classification Trees

• Trying to find the best partition by hand would be tremendously tedious.

• But computers are great at it.

• When creating a classification tree, the computer will check thousands of possible partitions, see how much it reduces entropy, and pick the best one.

Classification Trees

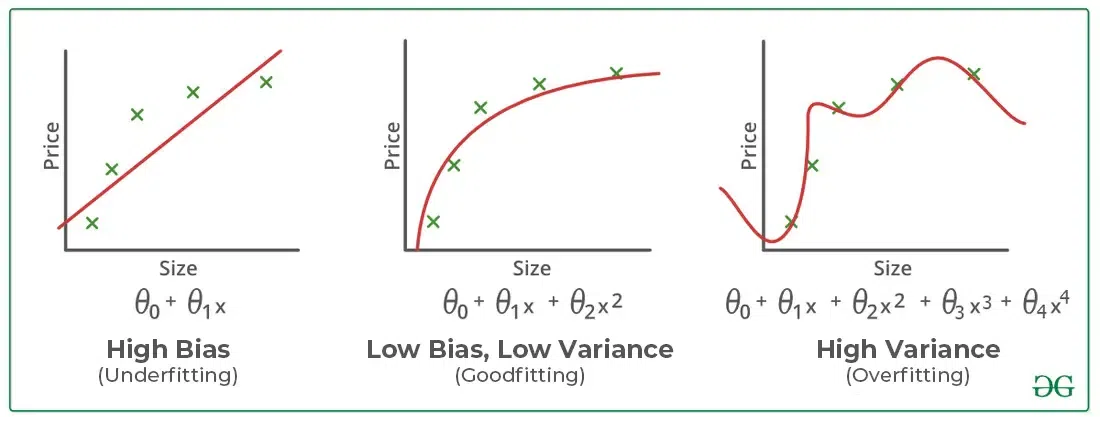
How Complex Should The Tree Get?

Bias-Variance Tradeoff

• It’s our old friend, the bias-variance tradeoff!

• Outside View (zero partitions) is biased.

• Inside View (lots of partitions) has higher variance, because your predictions are based on less data.

• Sweet spot is somewhere in the middle.

Bias-Variance Tradeoff

• In machine learning, this tradeoff is called overfitting vs. underfitting.

. . .

Next Time

• Next time, we’ll talk about how to hit that “sweet spot” between overfitting and underfitting.

• And we’ll show how you can harness the wisdom of crowds with machine learning models.

• Spoiler alert: we’re going to take a bunch of different classification trees and ask them to “vote” on the best prediction.

• The resulting machine learning model is called random forest.