Why Cities?
POLS 4641: The Science of Cities
Warmup
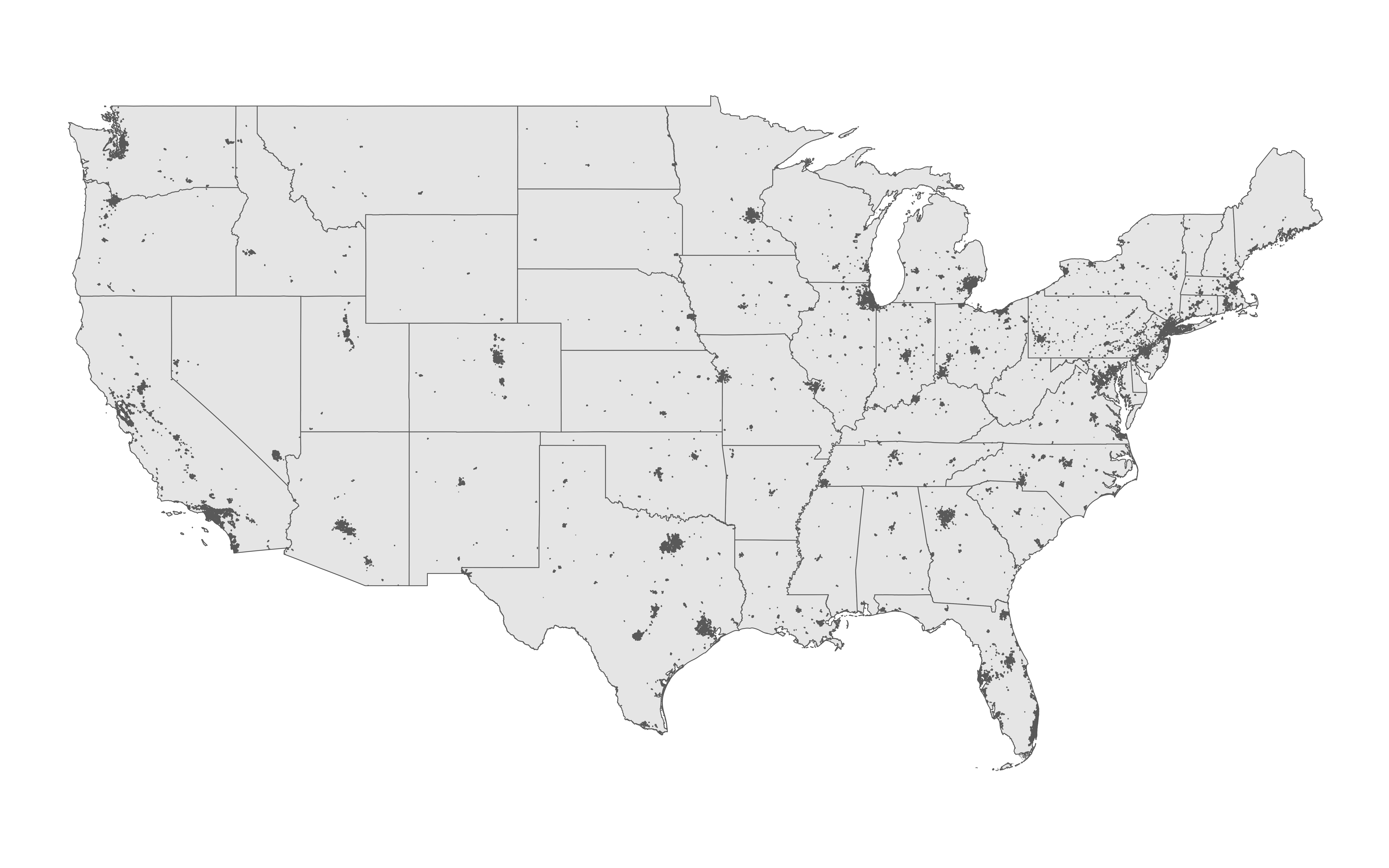
In the United States (minus Alaska and Hawaii), half of the population lives on roughly _____% of the land.
Warmup
In the United States (minus Alaska and Hawaii), half of the population lives on roughly 1% of the land.
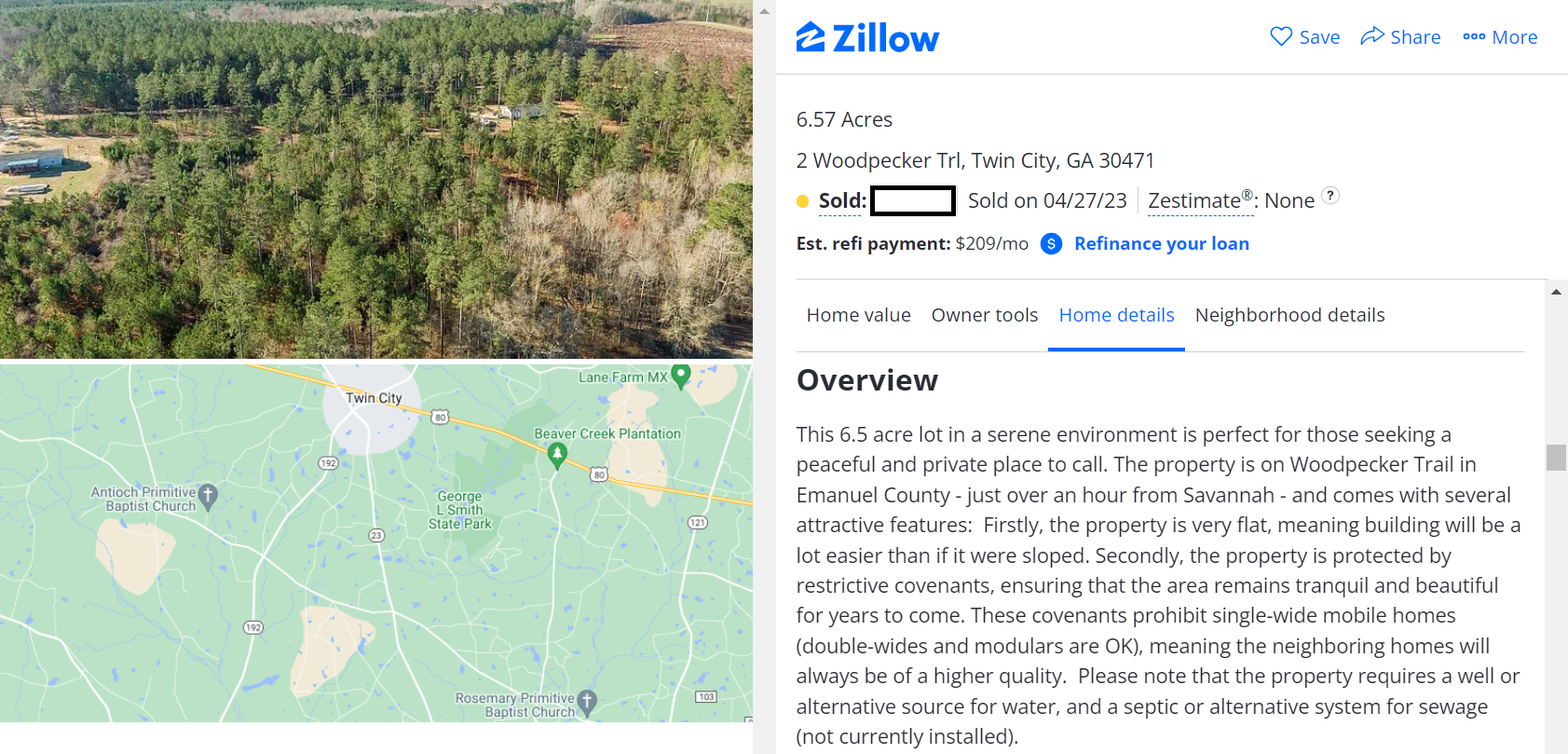
Land Values
Let’s play The Price Is Right. How much did this 6.5 acre lot sell for in 2023?
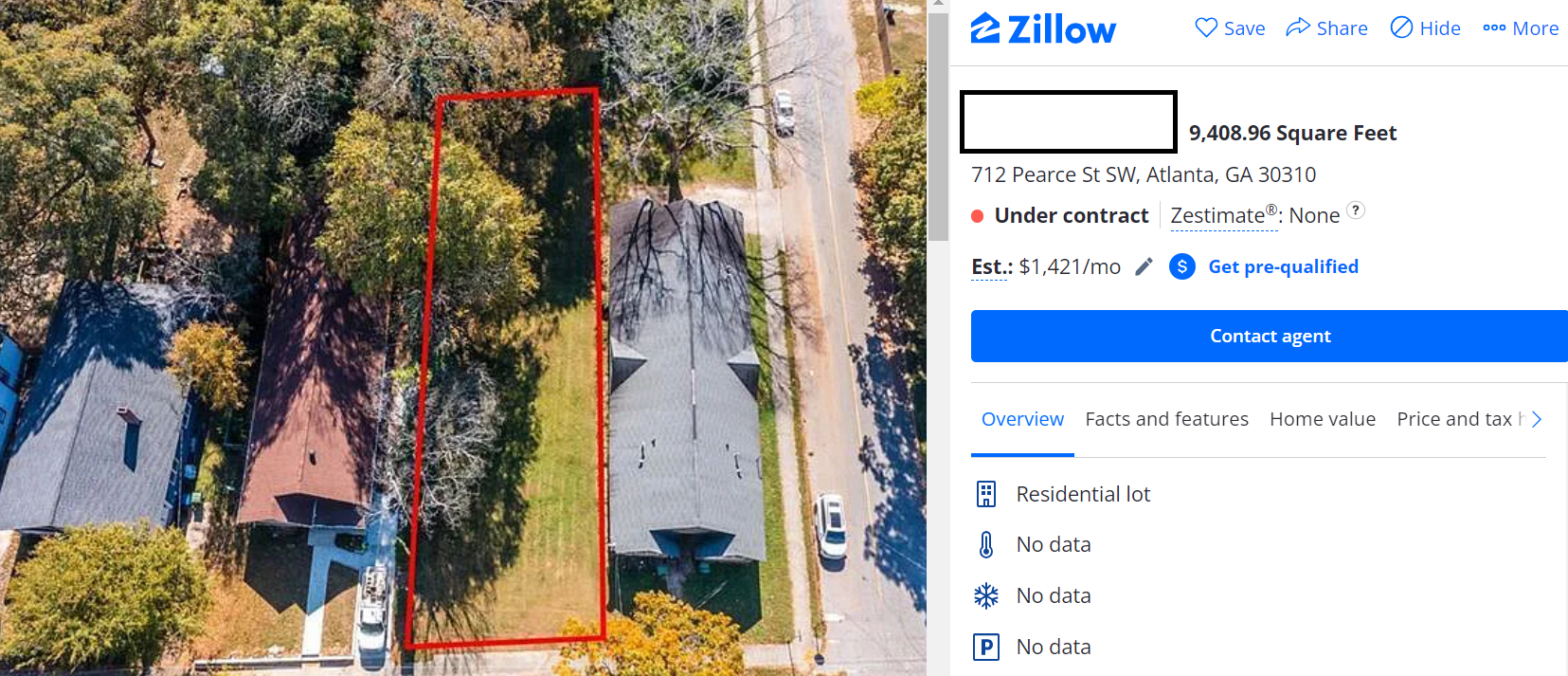
Land Values
Next item on The Price Is Right: this 9400 sq. foot lot (about 1/5 acre) in Atlanta.
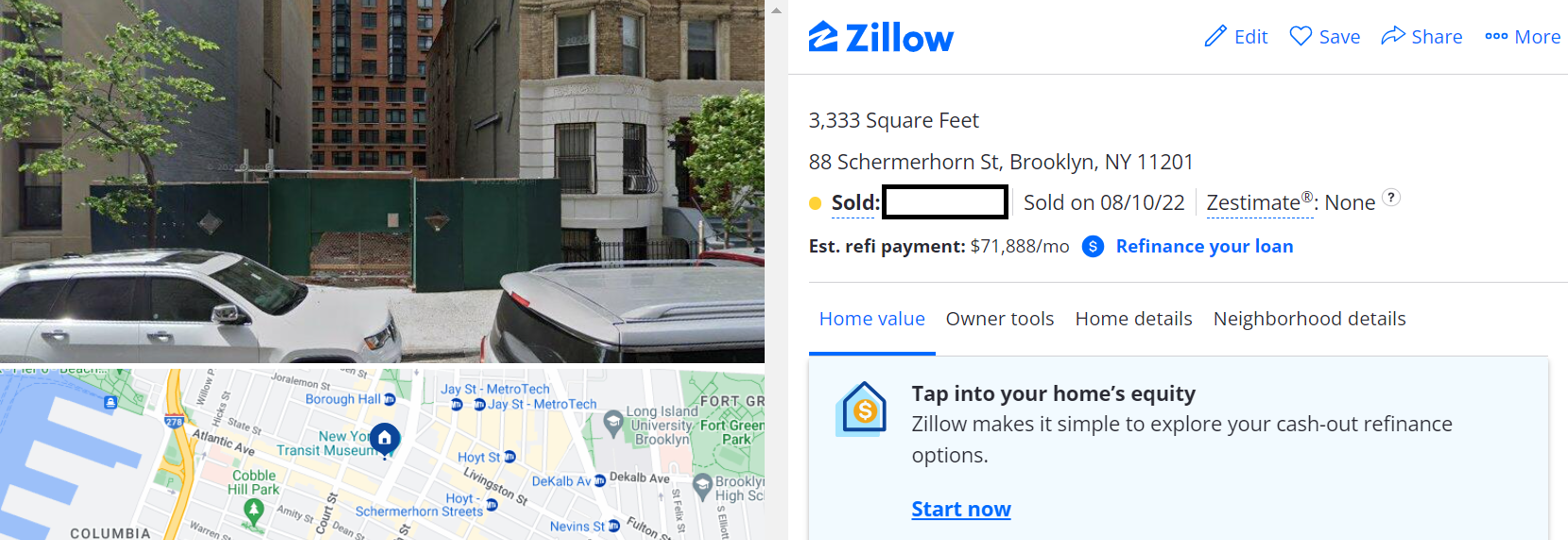
Land Values
Last item on The Price Is Right: this vacant lot in Brooklyn, NY.
Why Cities?
Why are some places on the map in such high demand compared to others? In a country with so much space, why do we crowd ourselves so much? And pay so much for it?
- To answer these questions, today we’ll introduce the concept of scale economies.
- Scale economies are the benefits that come from bringing large numbers of people together in one place.
- Three sources of scale economies that we’ll discuss:
Geometry
Fixed Costs
Network Effects
Scale Economies from Geometry
Scale Economies from Geometry
To illustrate this idea, let’s take a tour of some famous city walls.
- First Stop: Monteriggioni, Italy
- Second Stop: Carcassone, France
- Third Stop: Palmanova, Italy
- Fourth Stop: Bruges, Belgium
- Fifth Stop: Xi’An, China
- Final Stop: Paris, France
Scale Economies
Double the length of the wall, and you quadruple the size of the city you can protect.
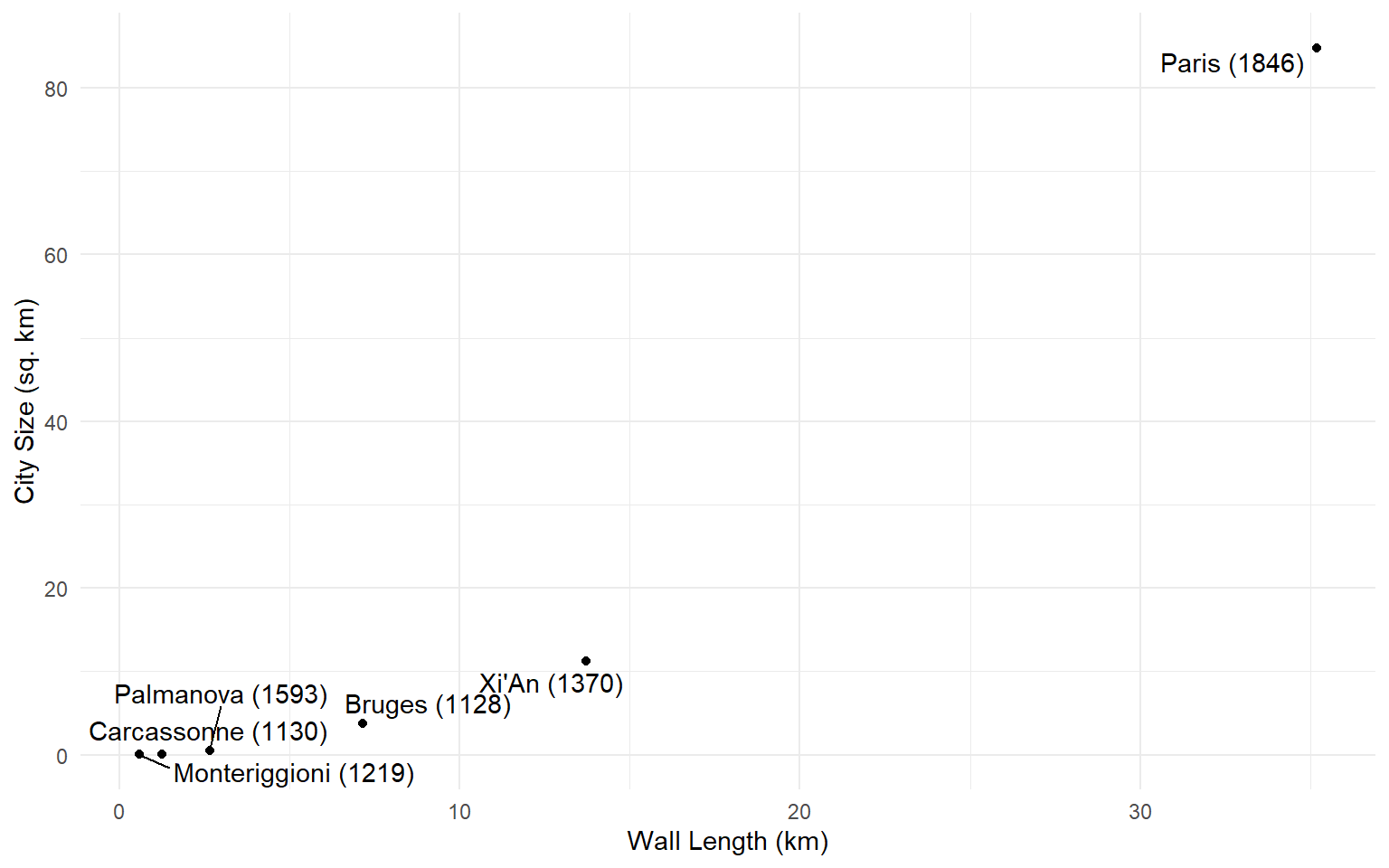
Scale Economies from Geometry
Double the length of the wall, and you quadruple the size of the city you can protect.
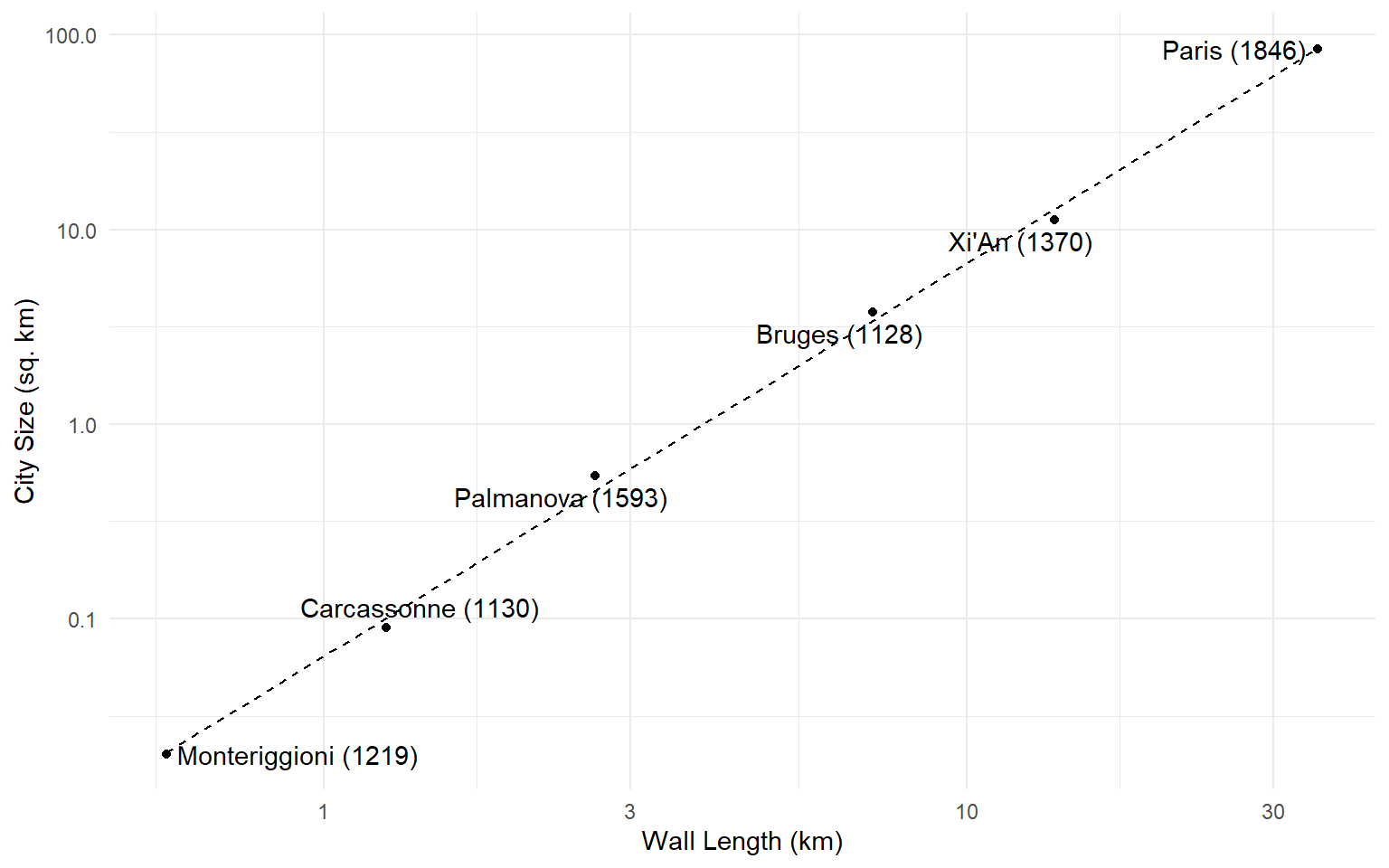
Scale Economies from Geometry
To see why, imagine a perfectly circular medieval city.

- The area of the city is \(A = \pi R^2\). The circumference is the length of the wall you need \((C = 2\pi R)\).
- Do some algebra, and you get \(A = \frac{1}{4\pi} C^2\).
Scale Economies
Double the length of the wall, and you quadruple the size of the city you can protect.
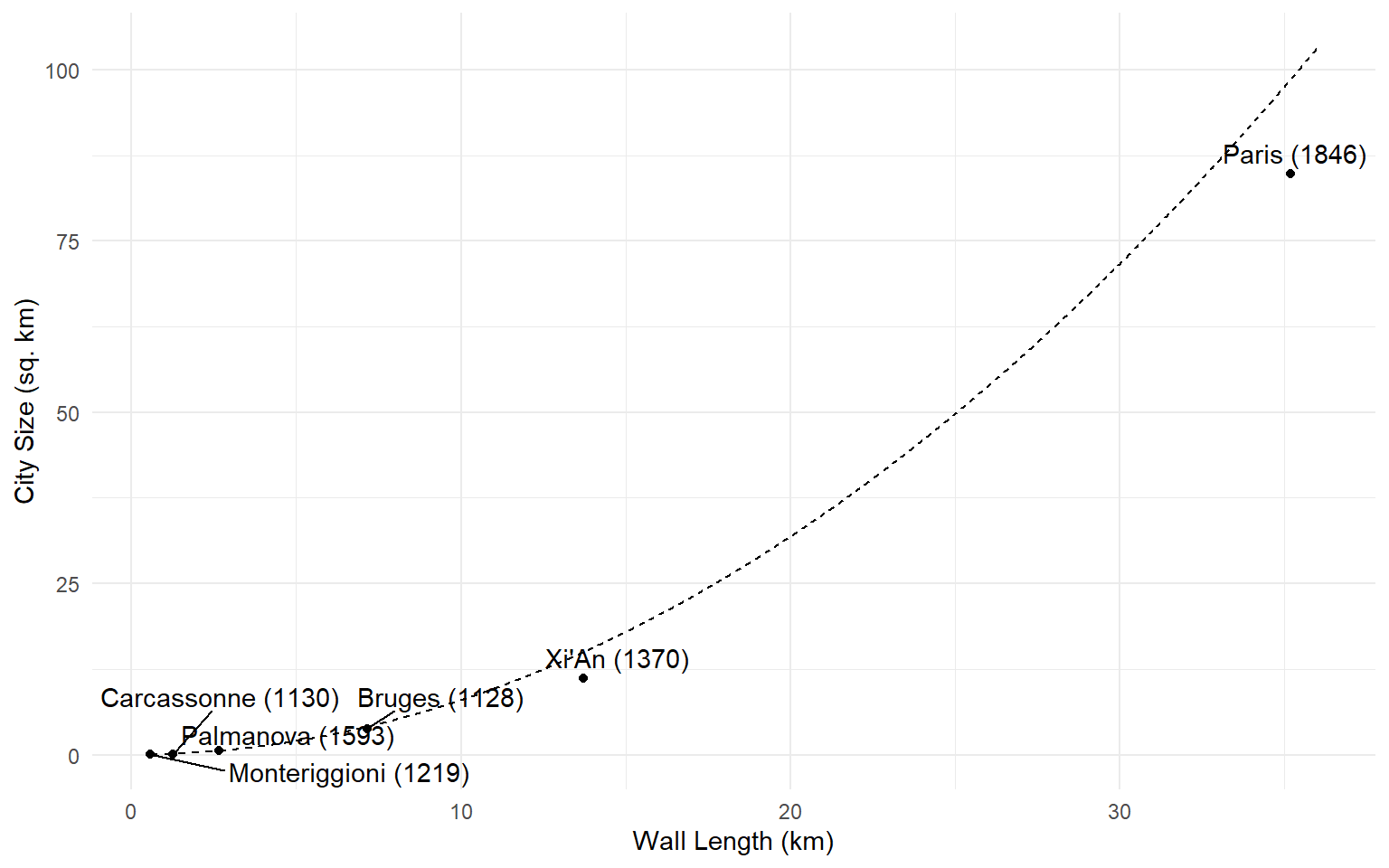
Scale Economies from Geometry
Put another way: big cities are cheaper to protect on a per-person basis. Double the size of a city, and you less than double the size of the necessary wall.
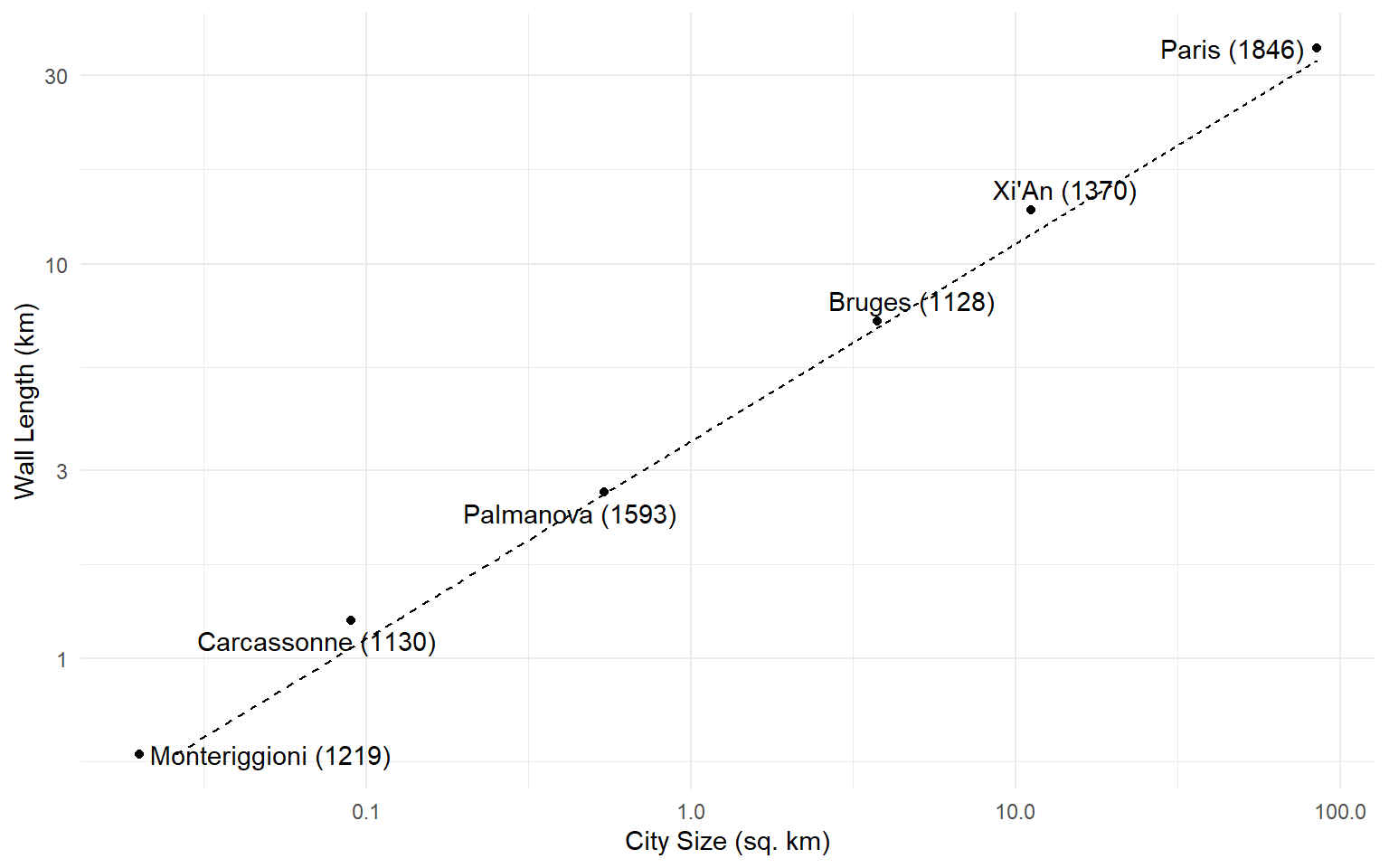
Scale Economies from Geometry
This sort of relationship holds for other (more modern) infrastructure as well, like streets.
.png)
Athens has 1,274 kilometers of streets for 128,000 people – roughly 10 meters per person.
Scale Economies from Geometry
Atlanta is 4x larger than Athens. About half a million people live in the city.
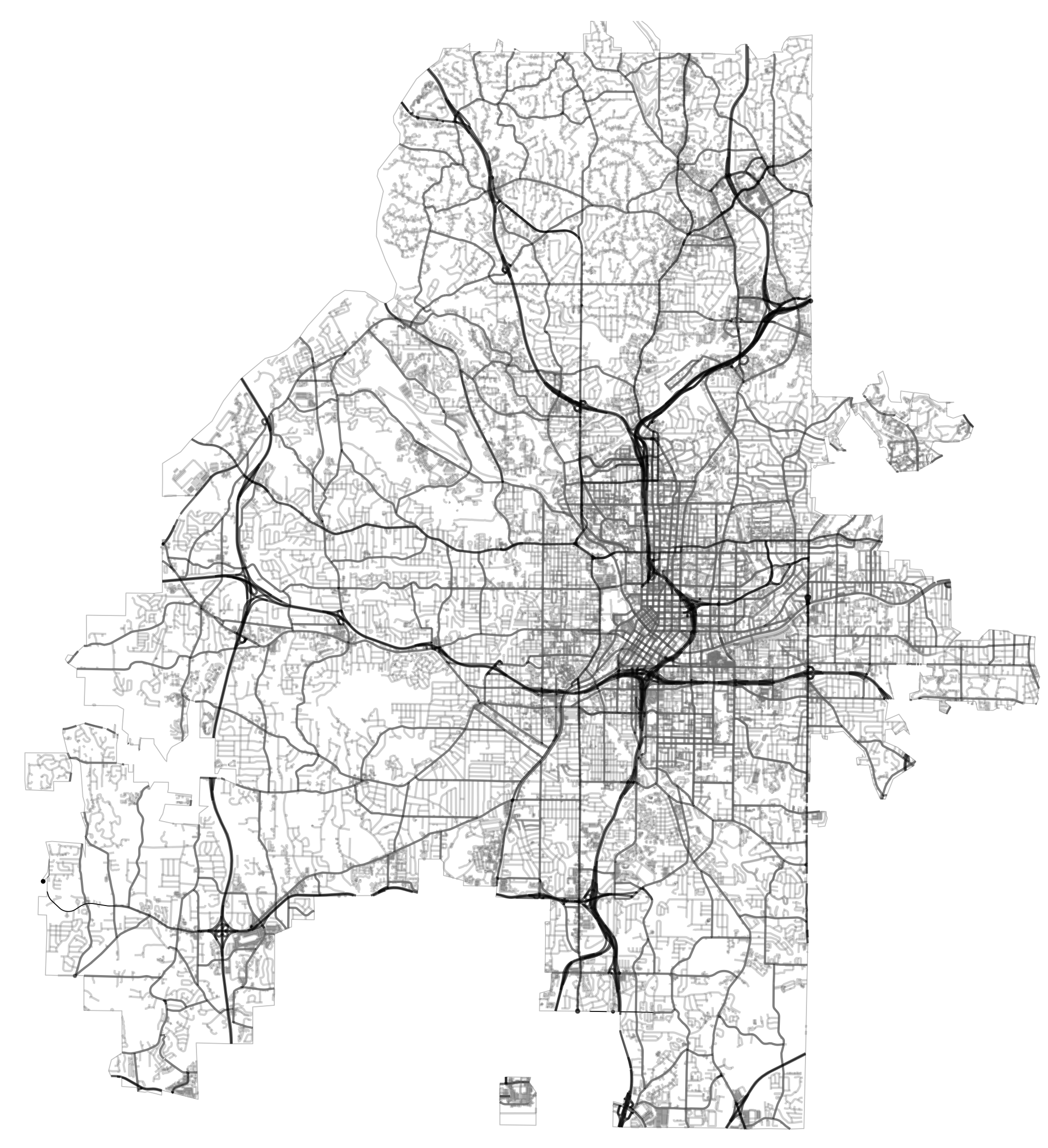
But it only has about twice the length of roadway (3,052 km) – 6 meters per person.
Scale Economies from Geometry
Philadelphia is about 3x bigger than Atlanta (1.6 million people).
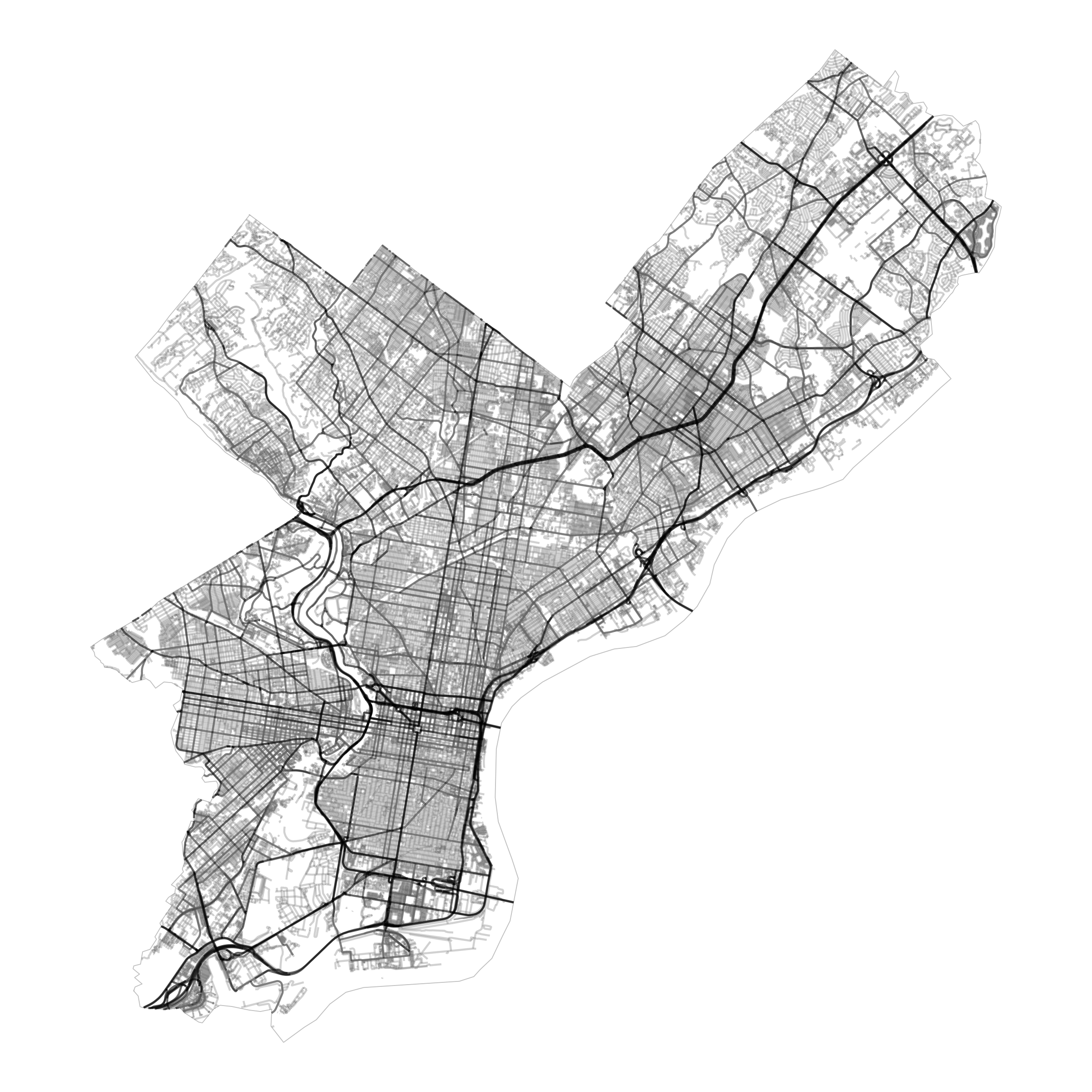
But it only has about 1.5x the length of roadways (4,539 km) – 3 meters per person.
Scale Economies from Geometry
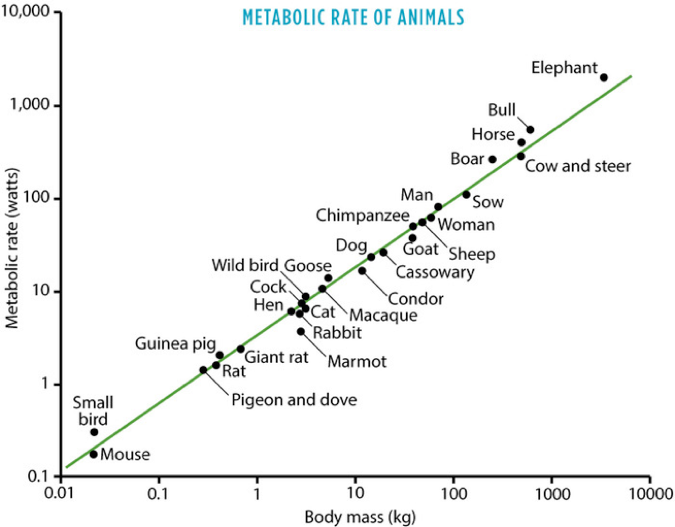
This is all eerily similar to the geometric scaling laws we see in nature.
- Double the size of an animal, and the energy necessary to keep it alive less than doubles.
Scale Economies from Fixed Costs
Scale Economies from Fixed Costs
Another source of increasing returns comes from the way businesses operate.

Each block of cheese costs you \(c\) dollars (marginal costs). You also have fixed costs of \(F\) dollars each month (rent, wages, electricity, etc.).
If you sell \(x\) blocks of cheese, then your average cost is:
\[ \frac{F + cx}{x} \]
Scale Economies from Fixed Costs
Let’s say your fixed costs are $10,000 and marginal costs are $5.
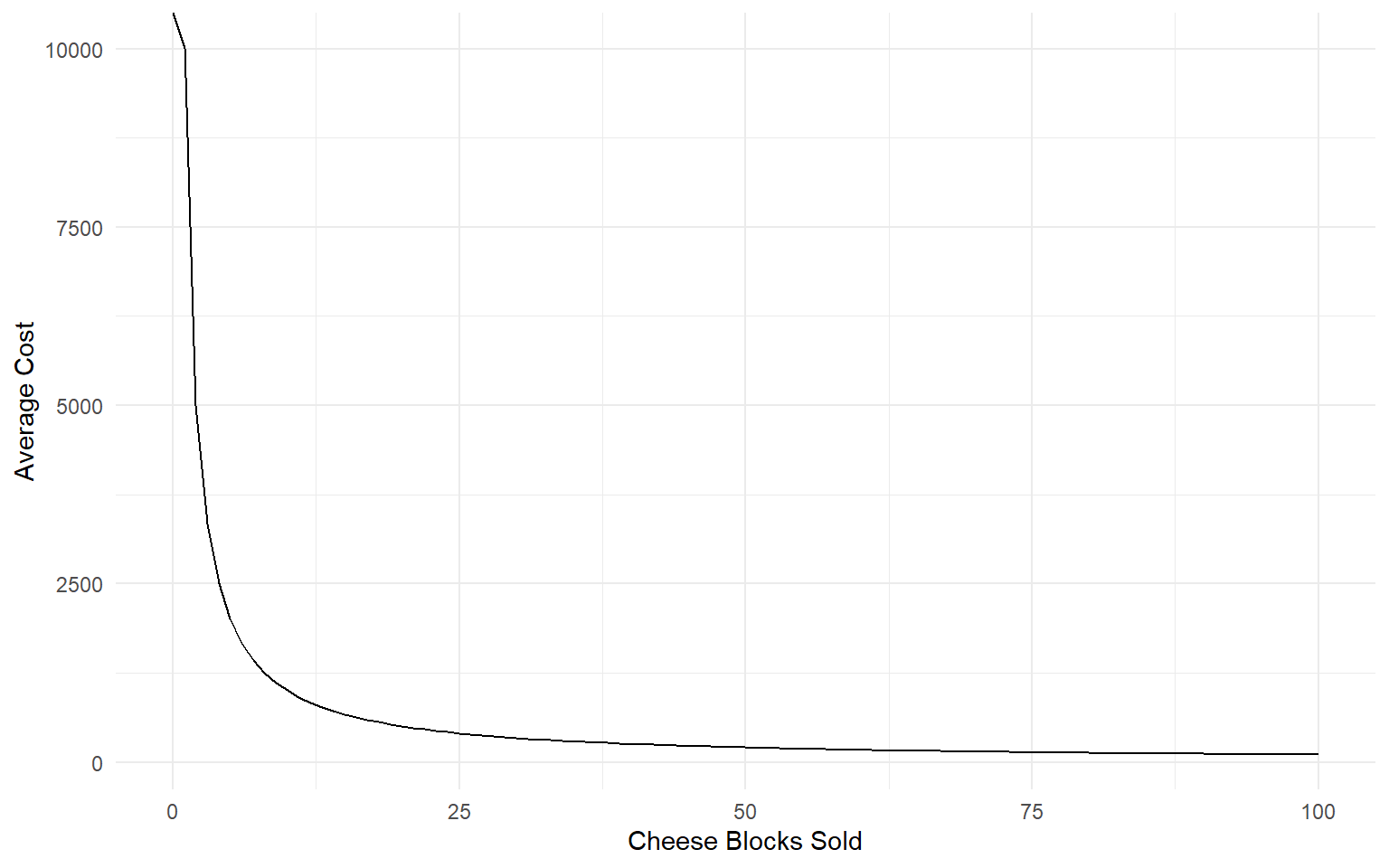
Unless you can sell cheese blocks for $5,000 each, you need a large number of customers in order to cover your fixed costs!
Scale Economies from Fixed Costs
This explains why:
Businesses with large fixed costs (major league sports stadiums, live theater, museums, zoos) can only operate in big cities.
Niche businesses (weird restaurants, esoteric bookstores, artisan cheese shops) typically operate in larger markets too.
- Doesn’t matter how many people visit your zoo. You’ve gotta feed that elephant 350 pounds of vegetation every day!
Scale Economies from Fixed Costs
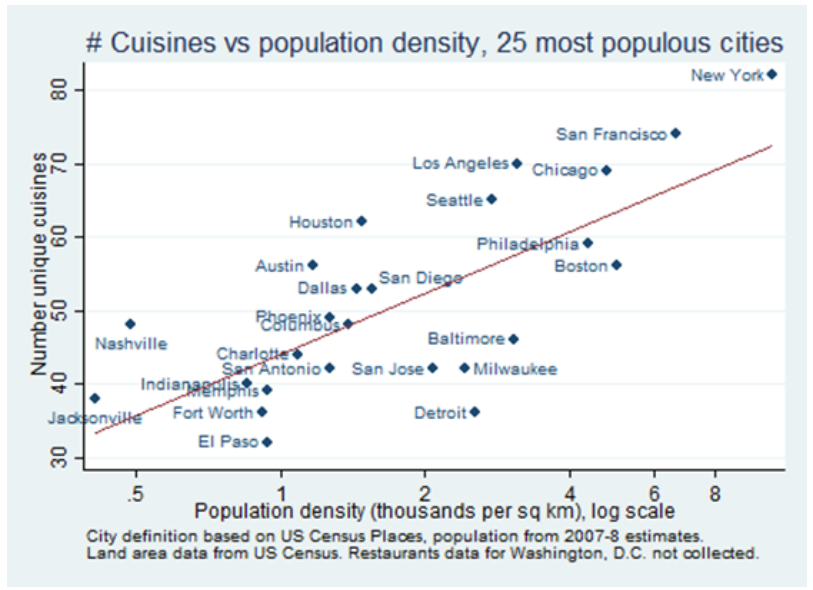
Scale Economies from Fixed Costs
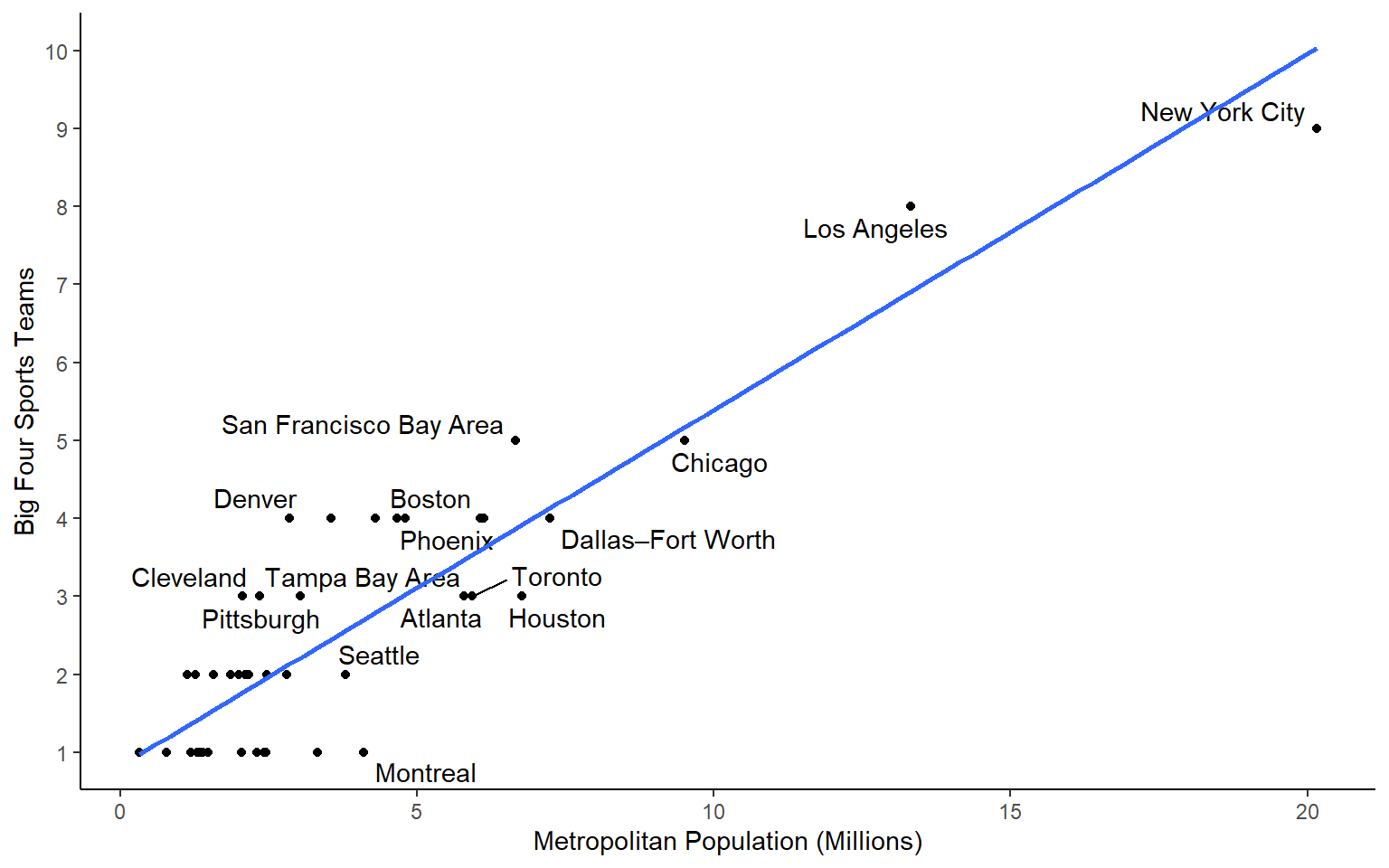
Scale Economies from Networks
Scale Economies from Networks
| Size of Network | Number of Connections |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
| 5 | 10 |
| 6 | 15 |
1 telephone is useless. There’s no one to talk to.
Larger networks are increasingly valuable, because the number of possible connections scales with \(n^2\).
Scale Economies from Networks
Metcalfe’s Law:
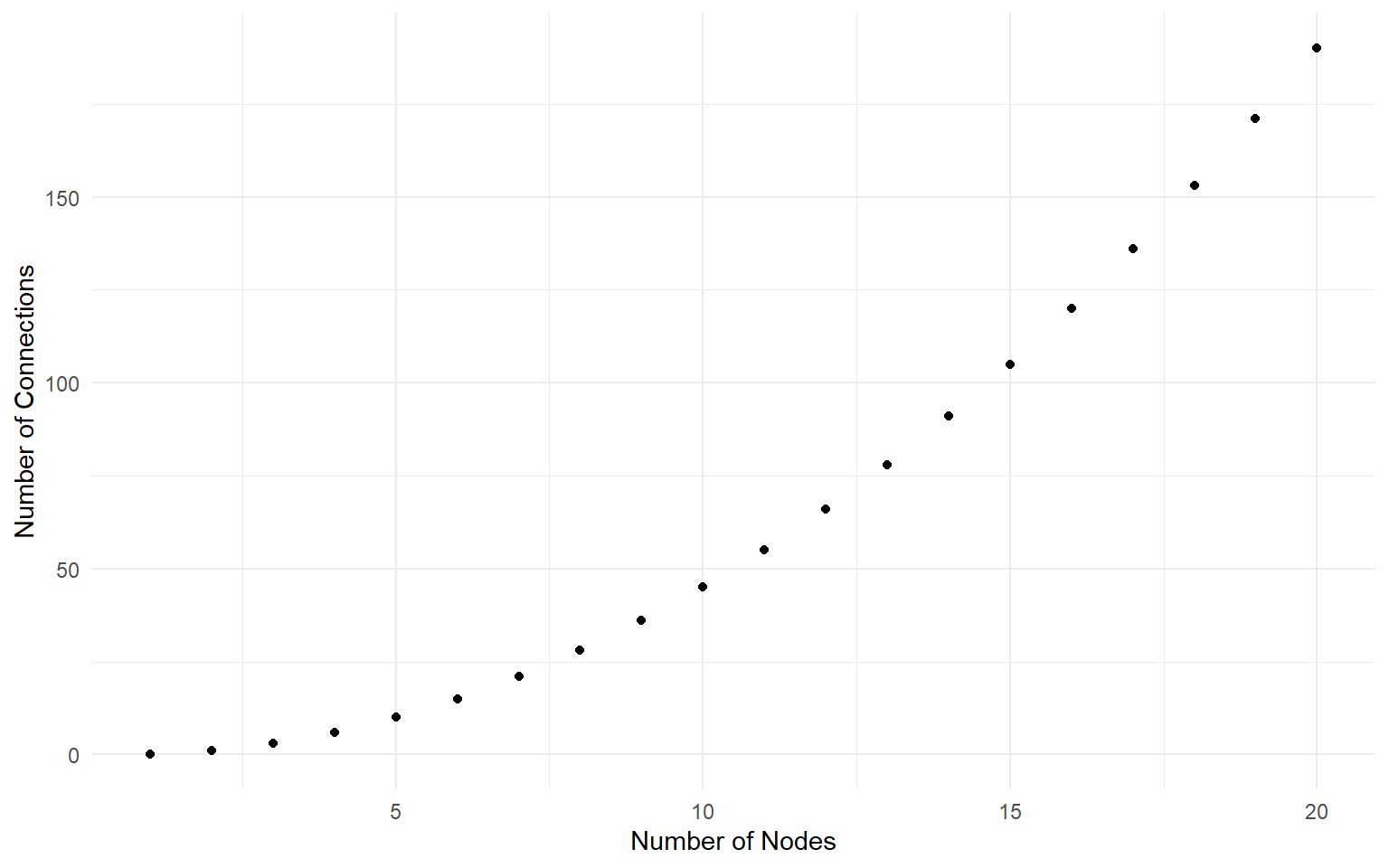
Scale Economies from Networks
- In a small town with 1,000 people, there are roughly 500,000 possible connections.
- There are about 30,000 undergraduates at UGA, or approximately 450 million possible friendships.
- In a city the size of New York (8 million), there are 32 trillion possible connections between people.
Anything that requires forging interpersonal connections (e.g. teamwork, social movements, dating) will be supercharged in big cities!
Scale Economies from Networks
Innovation and creativity come from people connecting with one another and sharing ideas. It’s no surprise, then, that big cities are hubs for innovation:
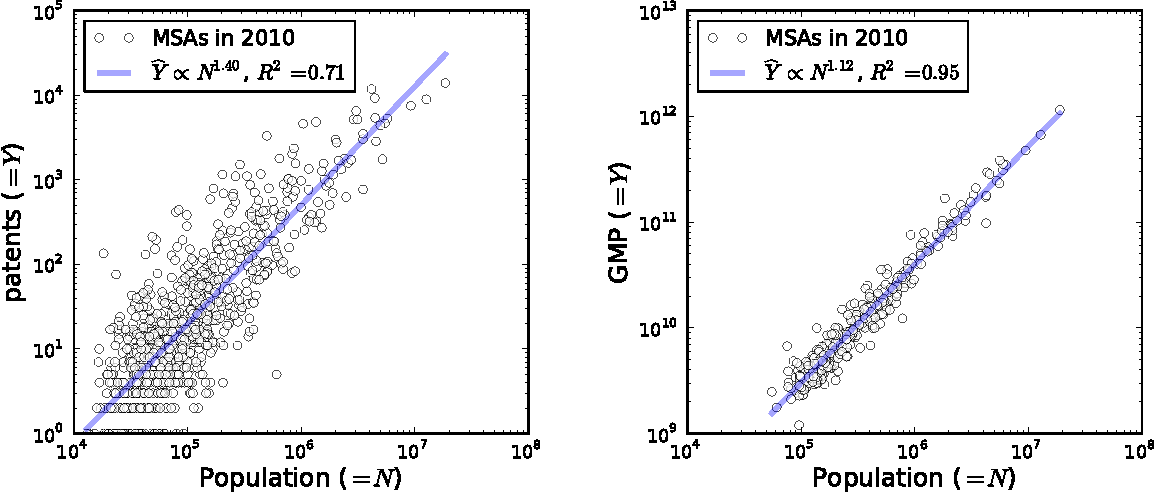
Agglomeration Effects
A Puzzle: Clusters of Industry
Scale economies explain why individual organizations would want to locate in large markets, but why would multiple, competing firms locate in the same place?
A Puzzle: Clusters of Industry
Scale economies explain why individual organizations would want to locate in large markets, but why would multiple, competing firms locate in the same place?
Agglomeration Economies
Why is it valuable to locate in the same city as your competitors?
Forward Linkages
Backward Linkages
Labor Market Pooling
Knowledge Spillovers