Calculus Essentials
Integrals and The Fundamental Theorem of Calculus
Area Under A Curve
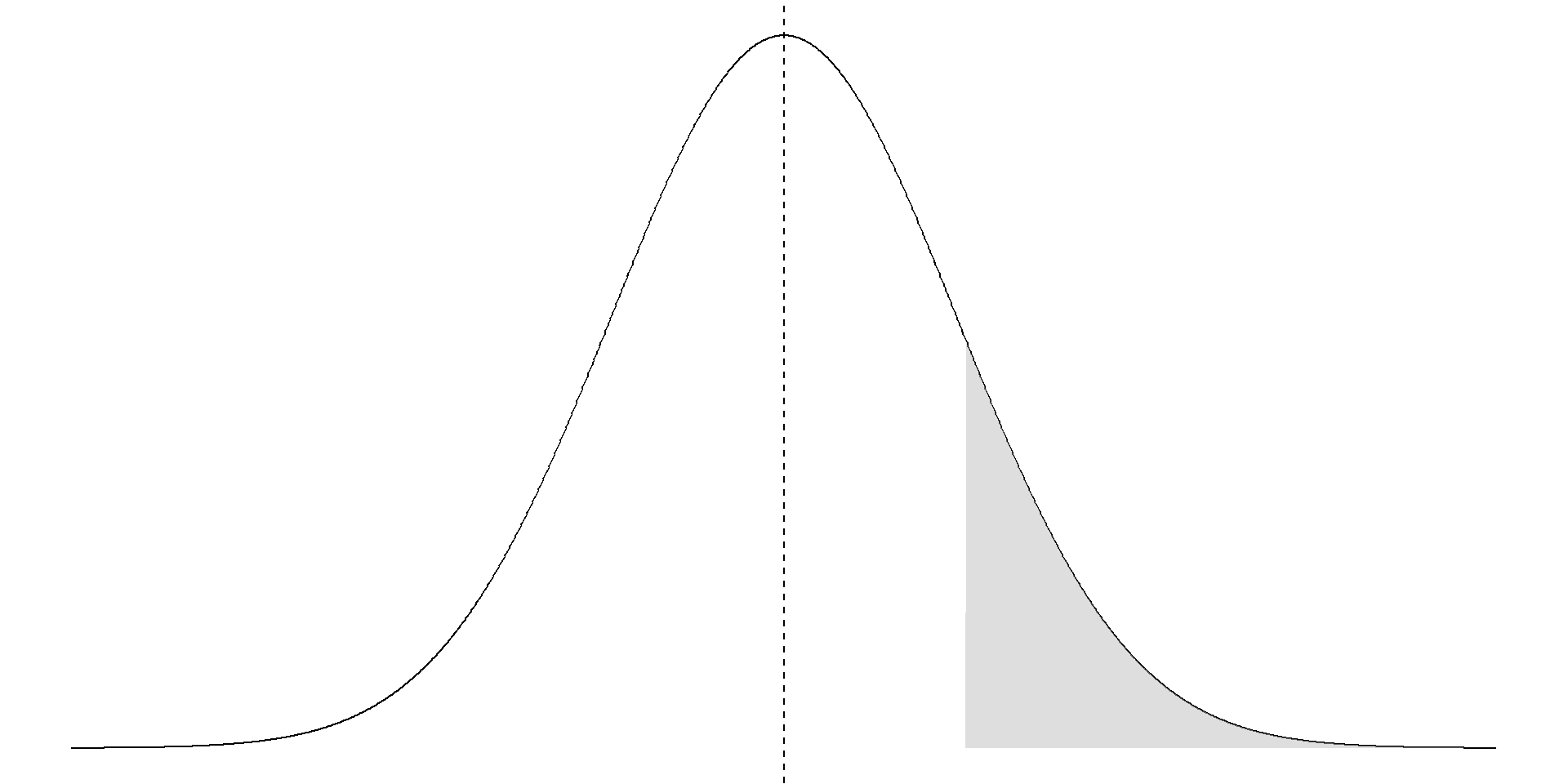
To compute a p-value, we need to know the area under the shaded part of the probability distribution function. We know that the area under the entire curve equals 1, but what fraction of that area is shaded below?
![]()
Area Under A Curve
The area of a rectangle is easy. \(A = bh\)
![]()
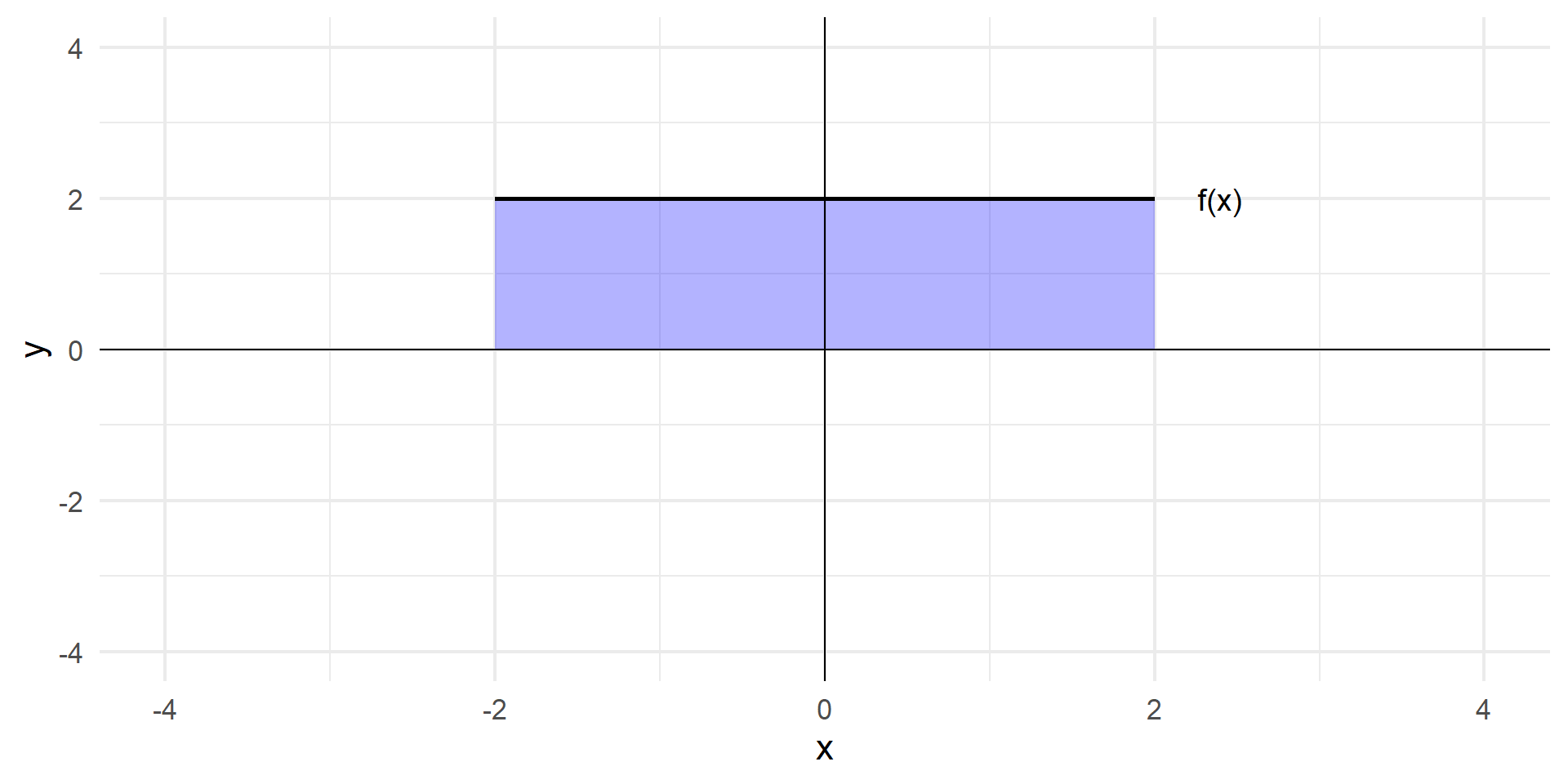
Area Under A Curve
Curves are harder. We didn’t learn this in geometry!
![]()
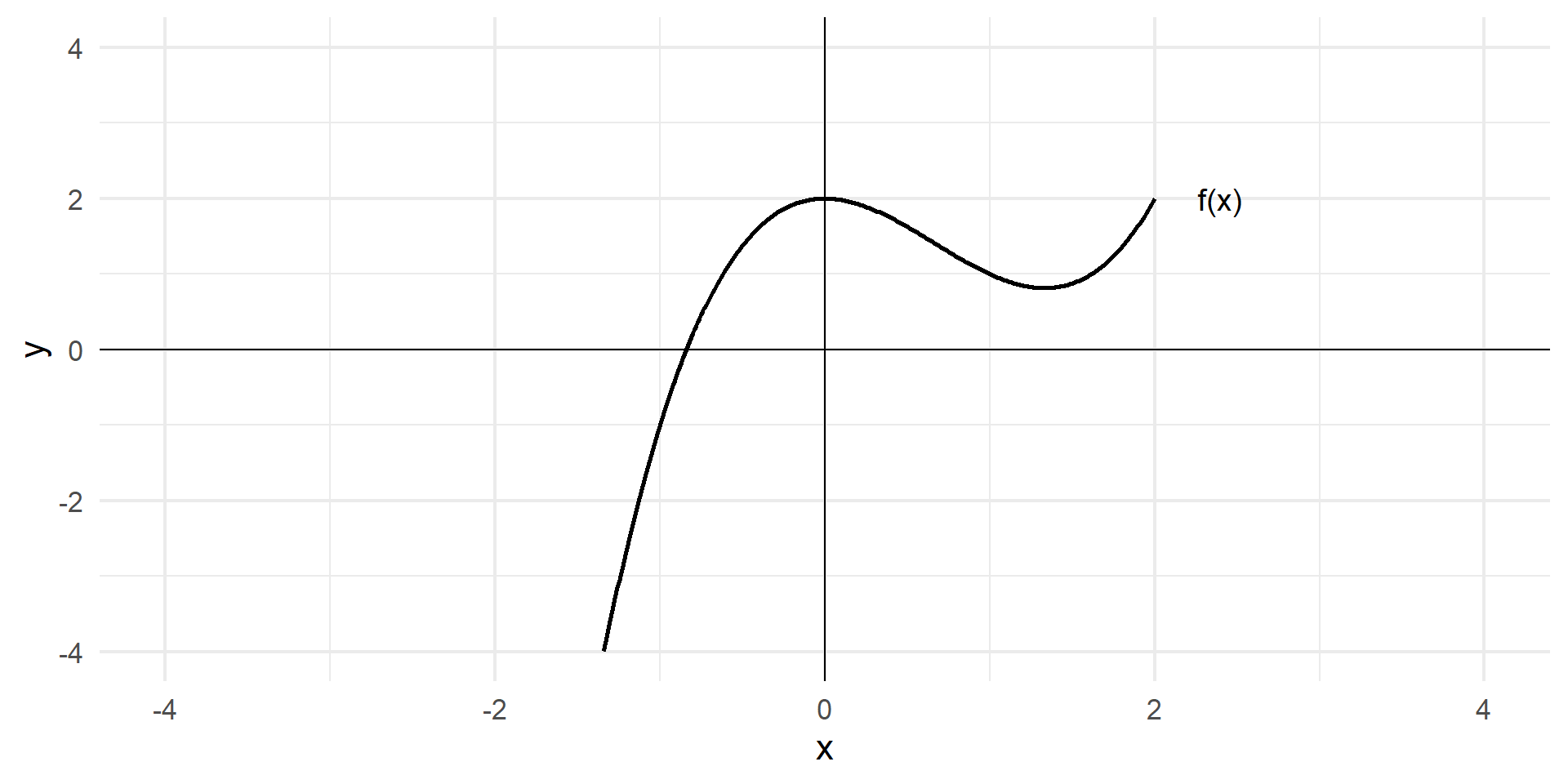
Area Under A Curve
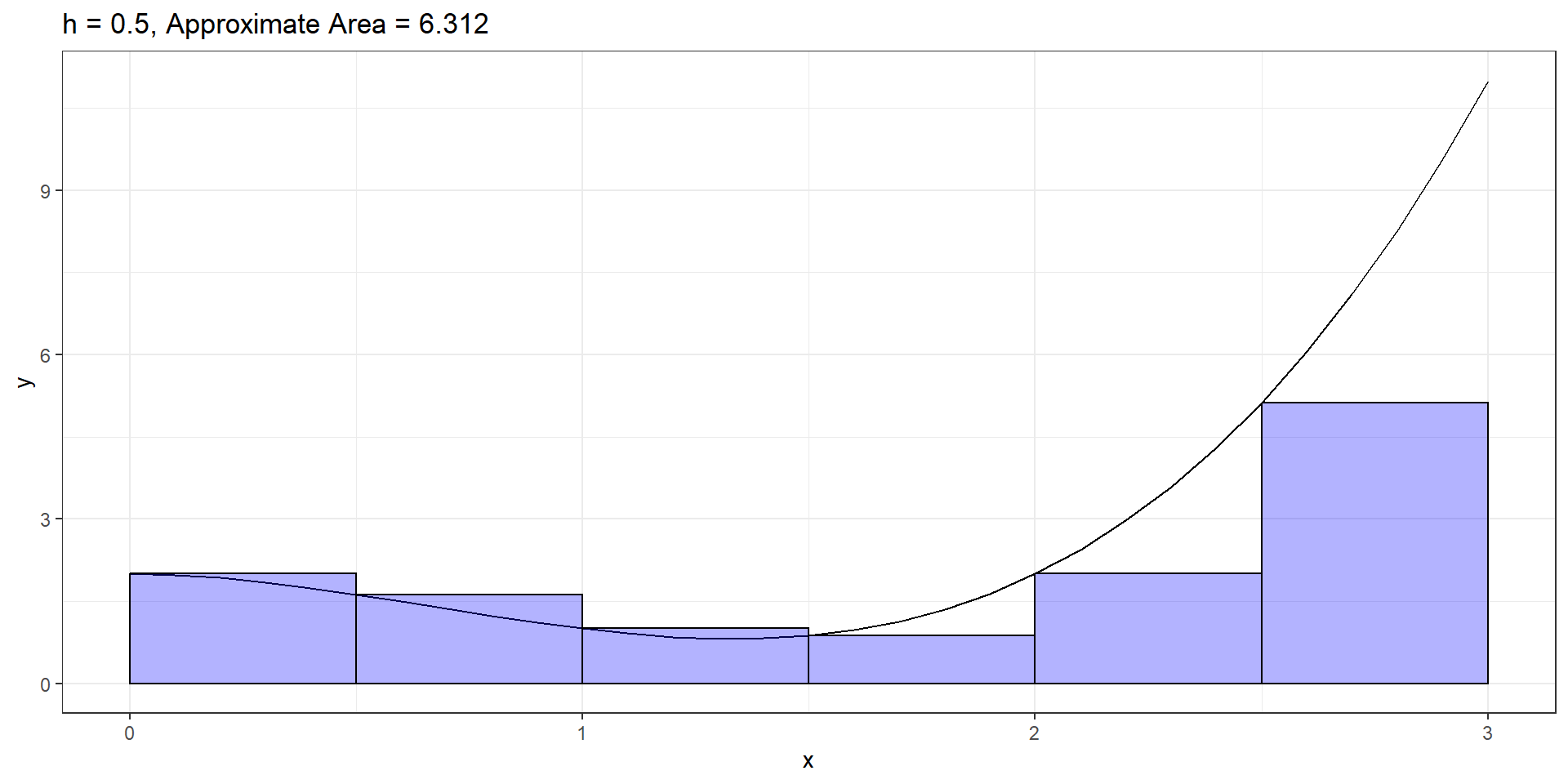
- With derivatives, we approximated a hard problem (the slope of a curve) using an easy problem (the slope of a line) by zooming in close enough.
- With integrals, we’ll use a similar trick.
- We approximate a hard problem (the area under a curve) using an easy problem (the area of a bunch of rectangles) by making the rectangles really thin.
Reimann Sum
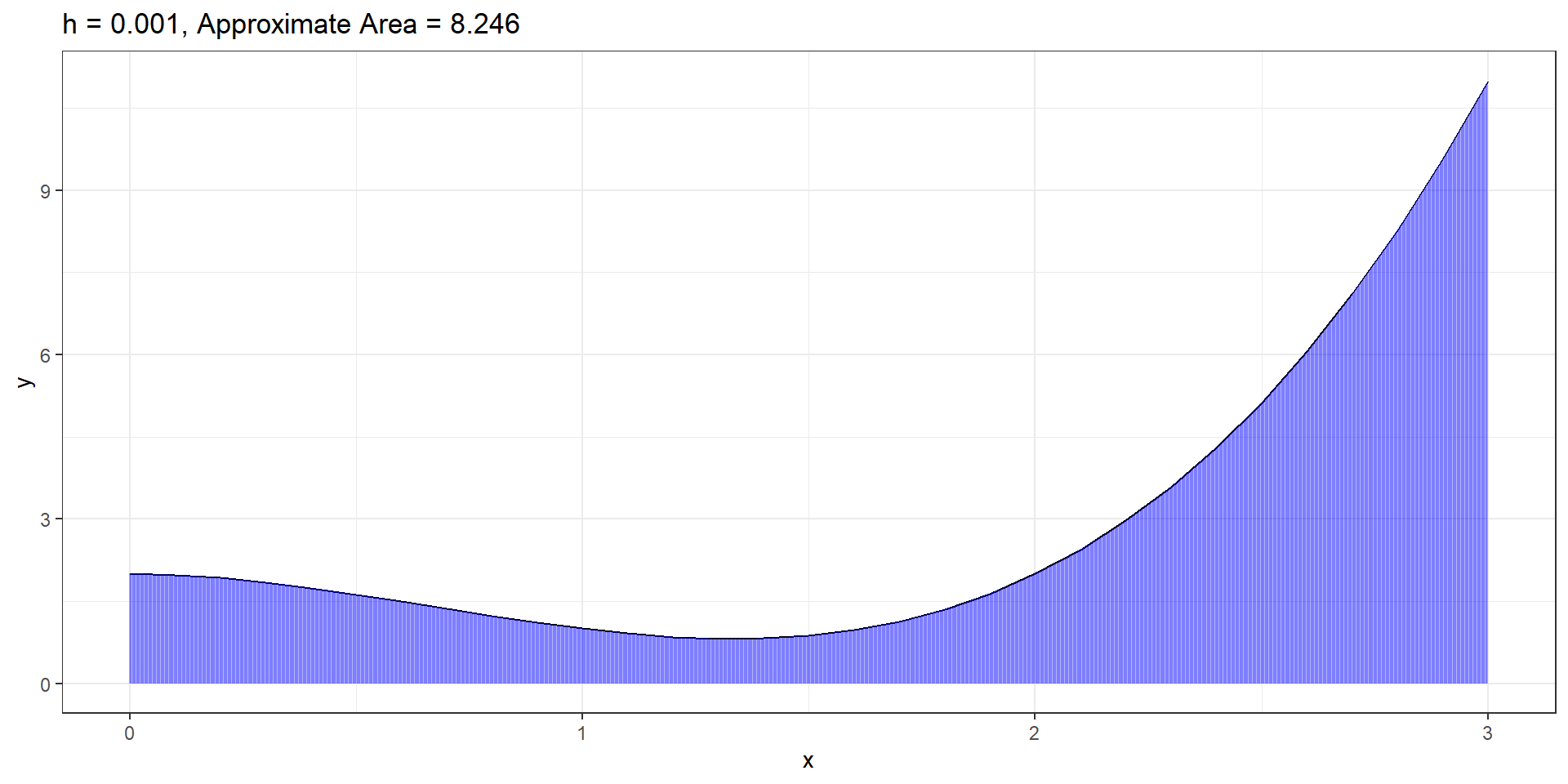
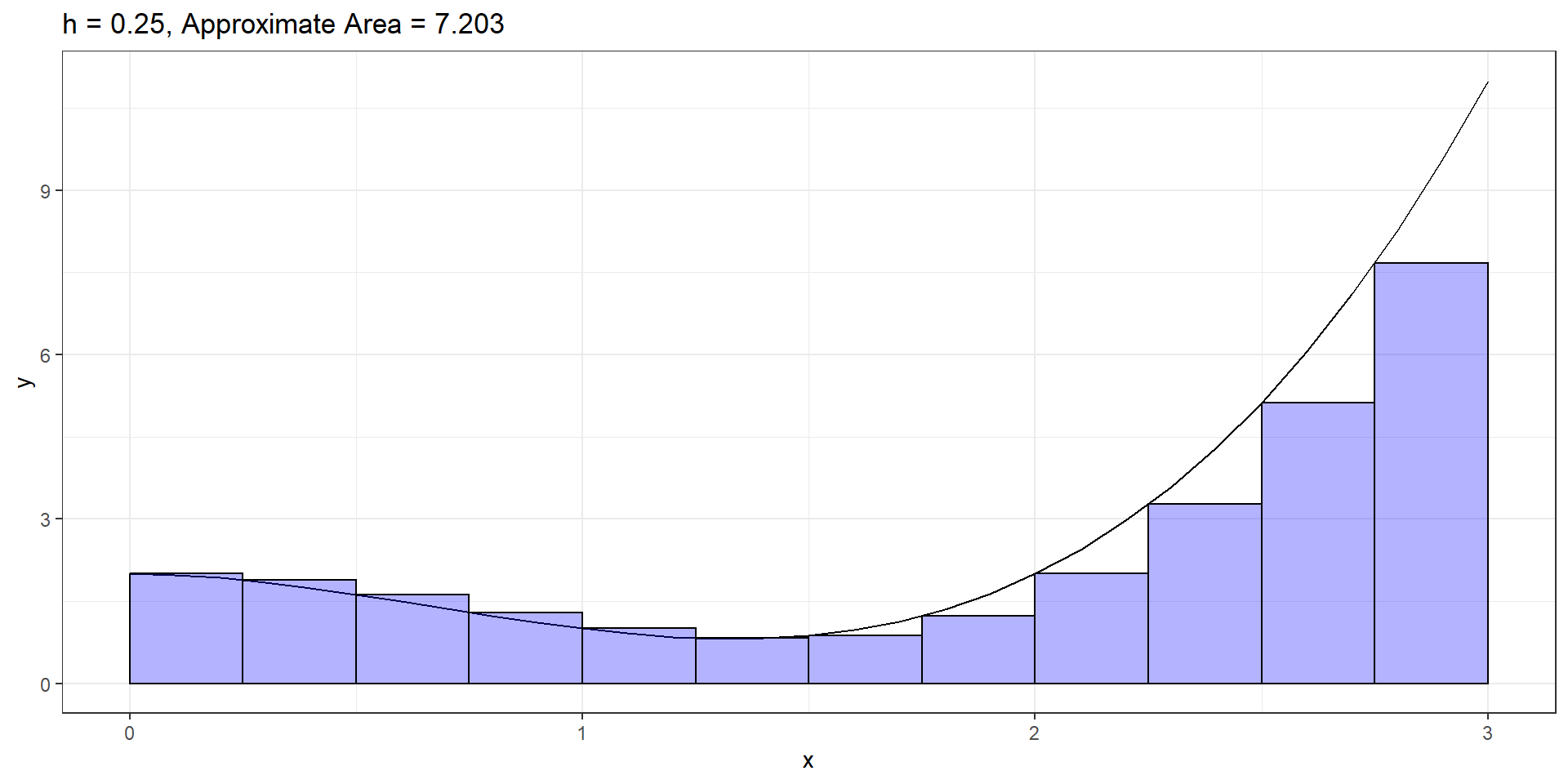
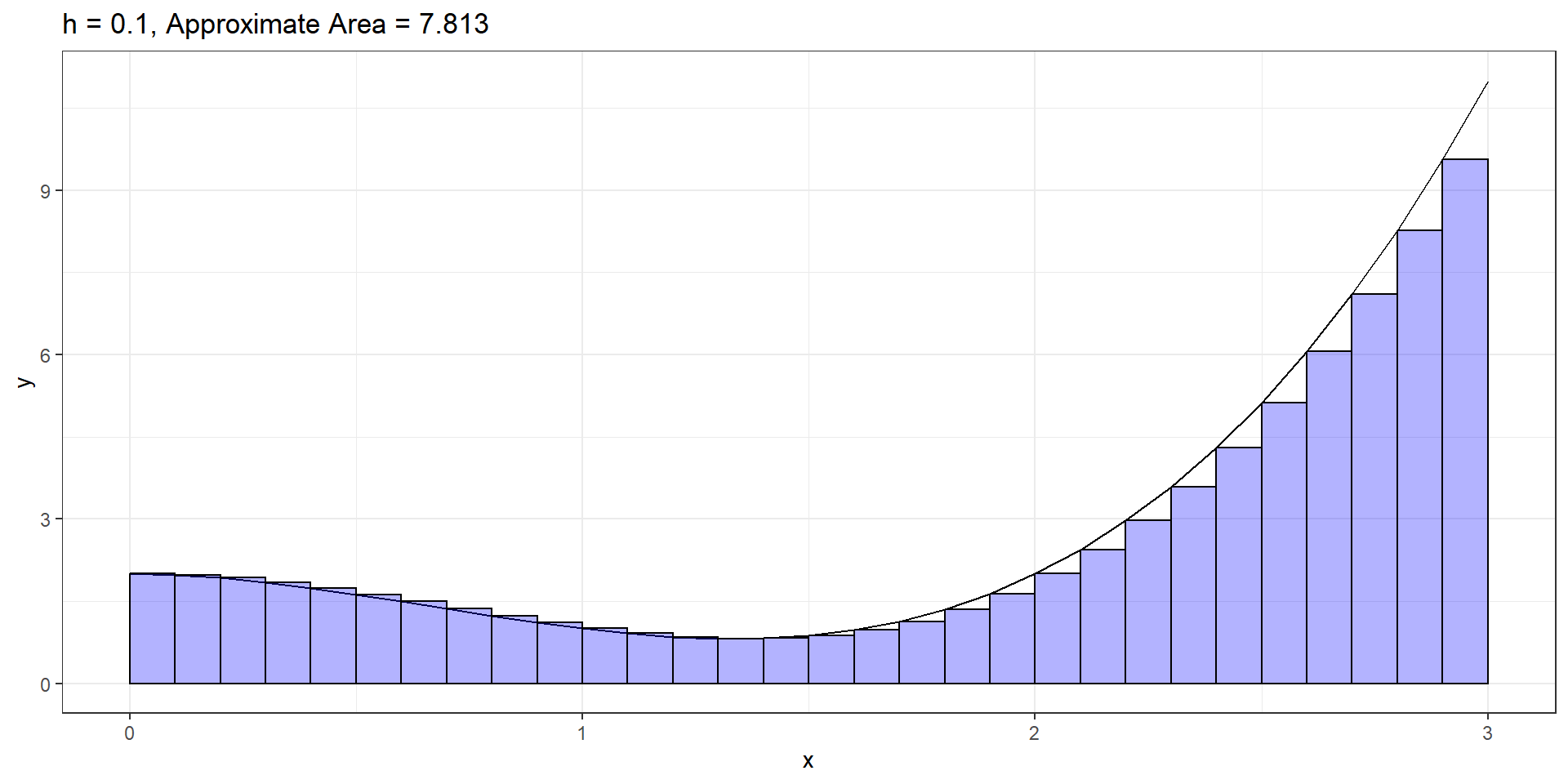
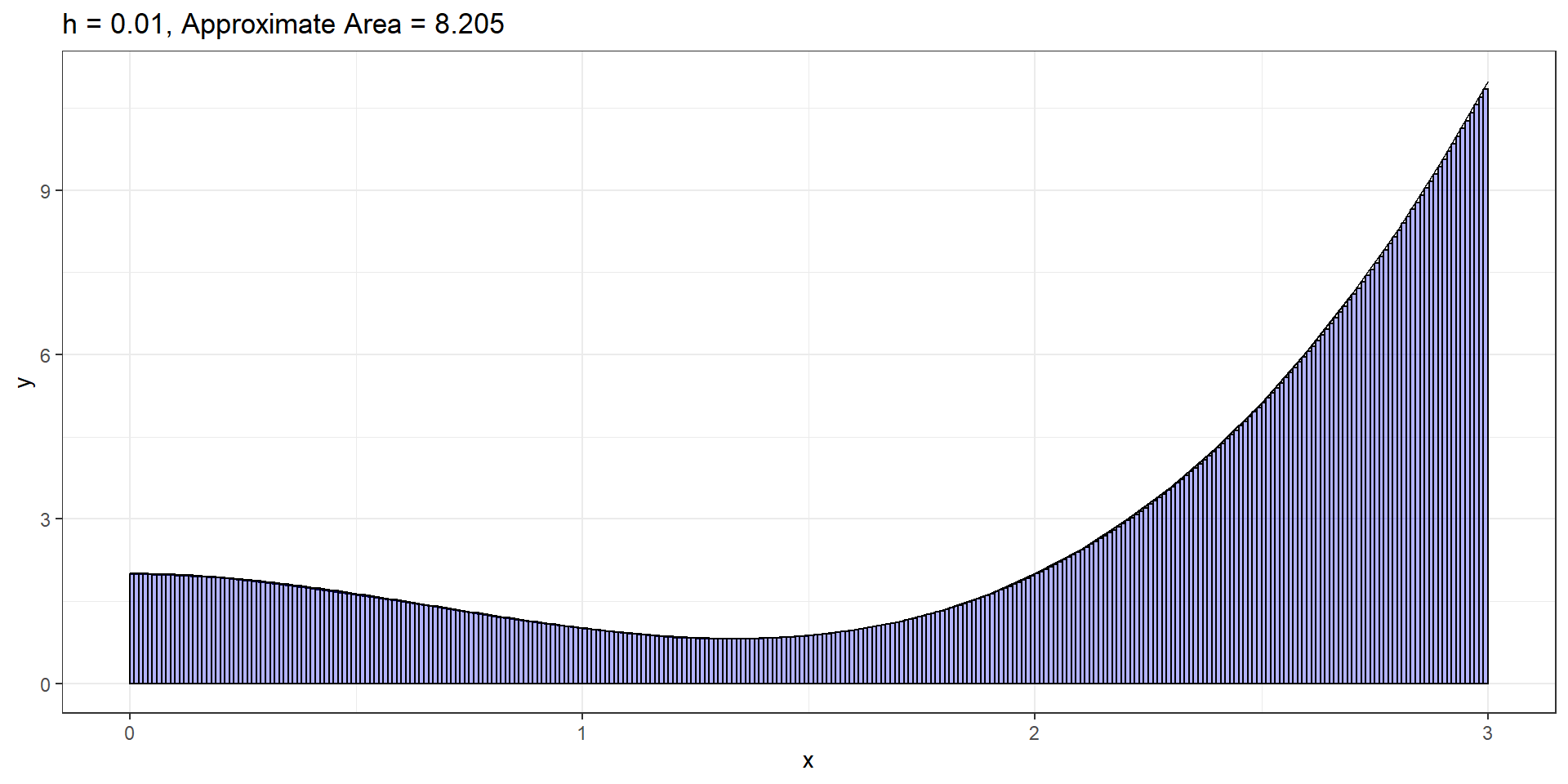
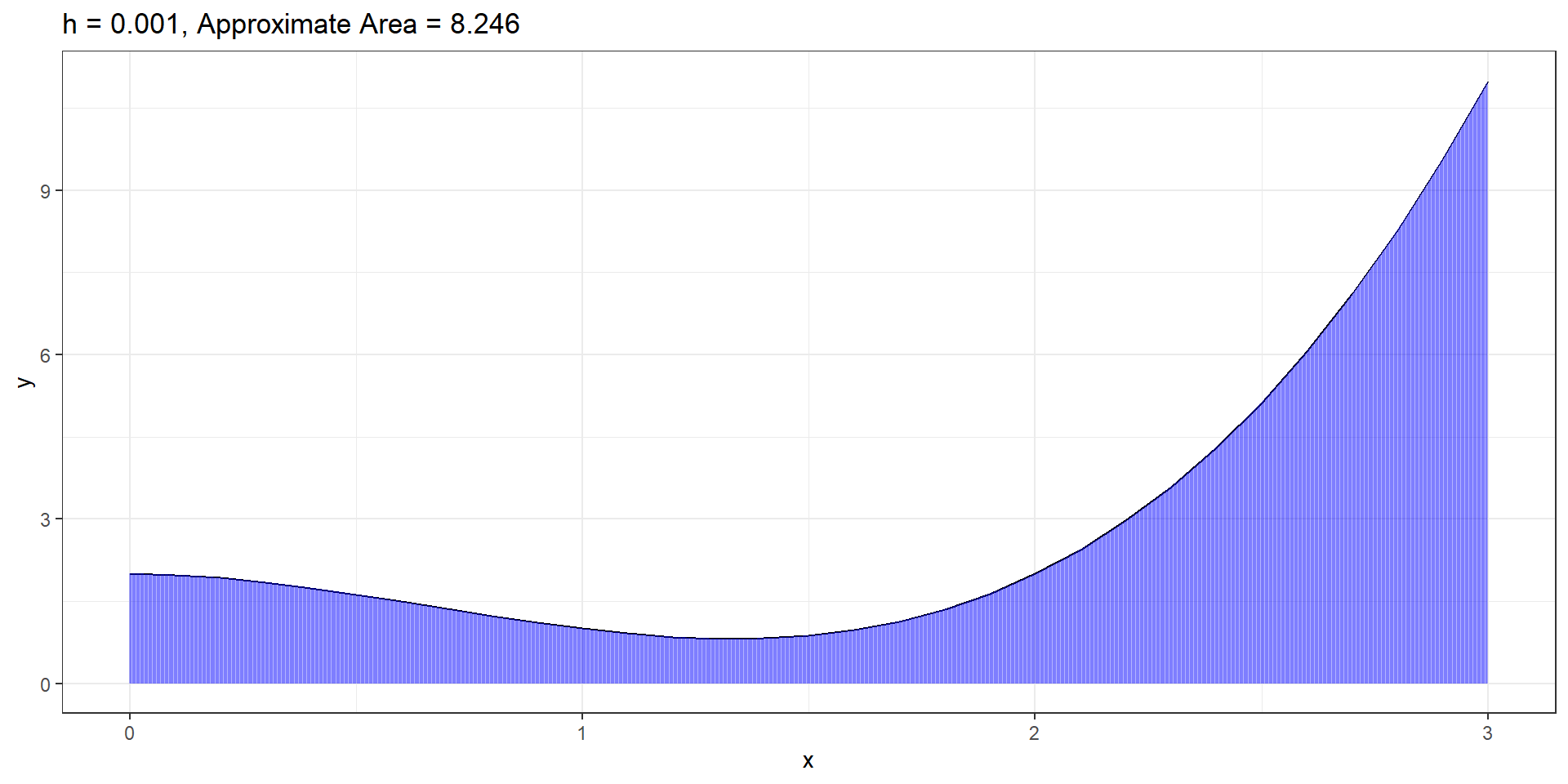
\(f(x) = x^3 - 2x^2 + 2\). Find area under curve from \(x=0\) to \(x=3\).
Reimann Sum
\(f(x) = x^3 - 2x^2 + 2\). Find area under curve from \(x=0\) to \(x=3\).
![]()
Reimann Sum
\(f(x) = x^3 - 2x^2 + 2\). Find area under curve from \(x=0\) to \(x=3\).
![]()
Reimann Sum
\(f(x) = x^3 - 2x^2 + 2\). Find area under curve from \(x=0\) to \(x=3\).
![]()
Reimann Sum
\(f(x) = x^3 - 2x^2 + 2\). Find area under curve from \(x=0\) to \(x=3\).
![]()
Integral Notation
\[\lim_{h \to 0} \sum f(x) \cdot h = \int f(x)dx \]
\(dx\) is an “infinitesimal” (infinitely small value).
So \(\int f(x)dx\) is the area of an infinite number of infinitely skinny rectangles.
If we want the area under a curve between \(a\) and \(b\), we denote it like so:
\[\int_a^b f(x)dx\]
The Area Function \(F(x)\)
There has to be an easier way to compute the area under a curve than taking the sum of an nearly infinite number of skinny rectangles…
What we want is a function \(F(x)\); let’s call it the area function.
The Area Function \(F(x)\)
As \(h\) approaches zero, our skinny rectangles should become a better and better approximation of this area function…
\[f(x) \cdot h = \lim_{h \to 0} F(x+h) - F(x)\]
Divide on both sides by \(h\).
\[f(x) = \lim_{h \to 0} \frac{F(x+h) - F(x)}{h}\]
Hey doesn’t that look familiar?
\(f(x) = F'(x)\). In other words, \(F(x)\) is the antiderivative.
The Fundamental Theorem of Calculus
\[\int_a^b f(x)dx = F(b) - F(a)\]
Finding the area under the curve and taking the antiderivative are equivalent operations!
Let’s Try It!
If \(f(x) = x\), find the area under the curve between \(x=0\) and \(x=4\).
![]()
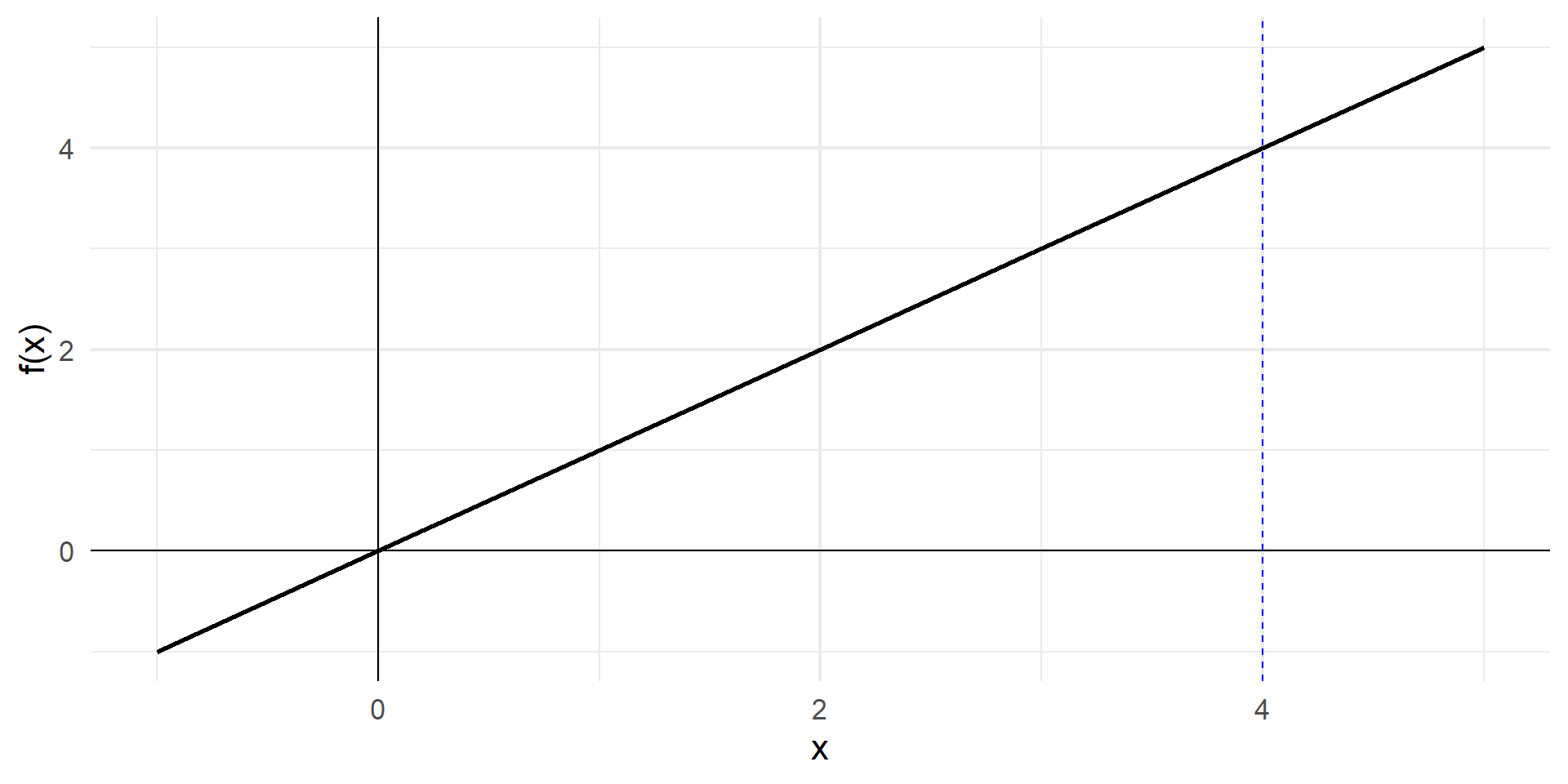
Let’s Try It!
If \(f(x) = x\), find the area under the curve between \(x=0\) and \(x=4\).
Use the Fundamental Theorem of Calculus
\[
\int_0^4 f(x)dx = F(4) - F(0)
\]
\(F(x) = \frac{1}{2}x^2 + C\)
\(F(4) - F(0) = \frac{1}{2}\cdot4^2 = 8\)
Now A Nonlinear Example…
If \(f(x) = x^3 - 2x^2 + 2\), find the area under the curve between \(x=0\) and \(x=3\).
\[\int_0^3 f(x)dx = F(3) - F(0)\]
\(F(x) = \frac{1}{4}x^4 - \frac{2}{3}x^3 + 2x + C\)
\(F(3) - F(0) = \frac{1}{4}3^4 - \frac{2}{3}3^3 + 2(3) - [\frac{1}{4}0^4 - \frac{2}{3}0^3 + 2(0)]\)
Now A Nonlinear Example…
That’s the same answer that we got from the skinny rectangles!
![]()
